DTMF信号的检测与识别
1. 程序设计思路与框图
1.1 FFT直接计算
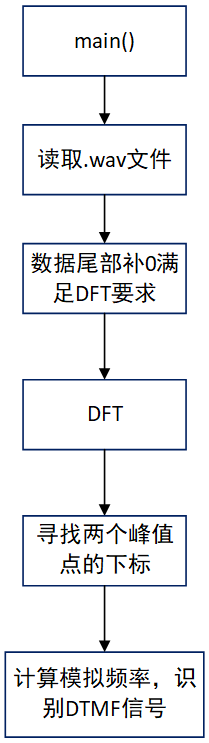
利用FFT计算输入的信号的DFT频域信息,并找到两个峰值频率点,从而检测DTMF信号。
数据预处理,作业给定的为.wav文件,其中数据为16bit的short类型,文件指针偏移40个字节的位置记录了wav数据块的字节数,调用read函数将之后的数据读入到数组中。
编写类FFTMethod,调用第一次作业编写的时域基2DFT对音频信号做FFT变换。找到频域中两个峰值对应的数字角频率,从而计算得到模拟角频率,找到对应的DTMF信号
程序框图
1.2 Goertzel 算法
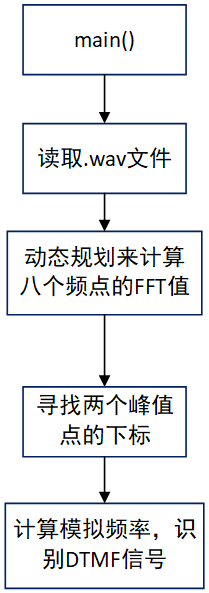
计算FFT包含了信号整个频域的信息,而我们只关注DTMF信号的八个特定频率,因此算法存在冗余。在FFT中如果我们只关注某一个特定的数字角频率,$X[k] = \sum_{n = 0}^{N- 1}x[m]W_n^{m -N}$,其可以视为$x[n]$通过冲激响应为$W_N^{-nk}$的LTI系统在N时刻的取值。第k个频点对应的差分方程为:
$$
V_k[n] = 2cos(\omega_k)V_k[n - 1] - V_k[n-2] + x[n] \
X_k[n] = V_k[n] - W_N^k[n - 1], v[-1] = v[-2] = 0
$$
其本质是一个动态规划的过程,由递推关系可以得到n时刻的状态,从而确定该频点的FFT。得到八个特定频点的FFT值后,选择两个峰值,从而确定DTMF信号。
1.3一串DTMF信号的识别
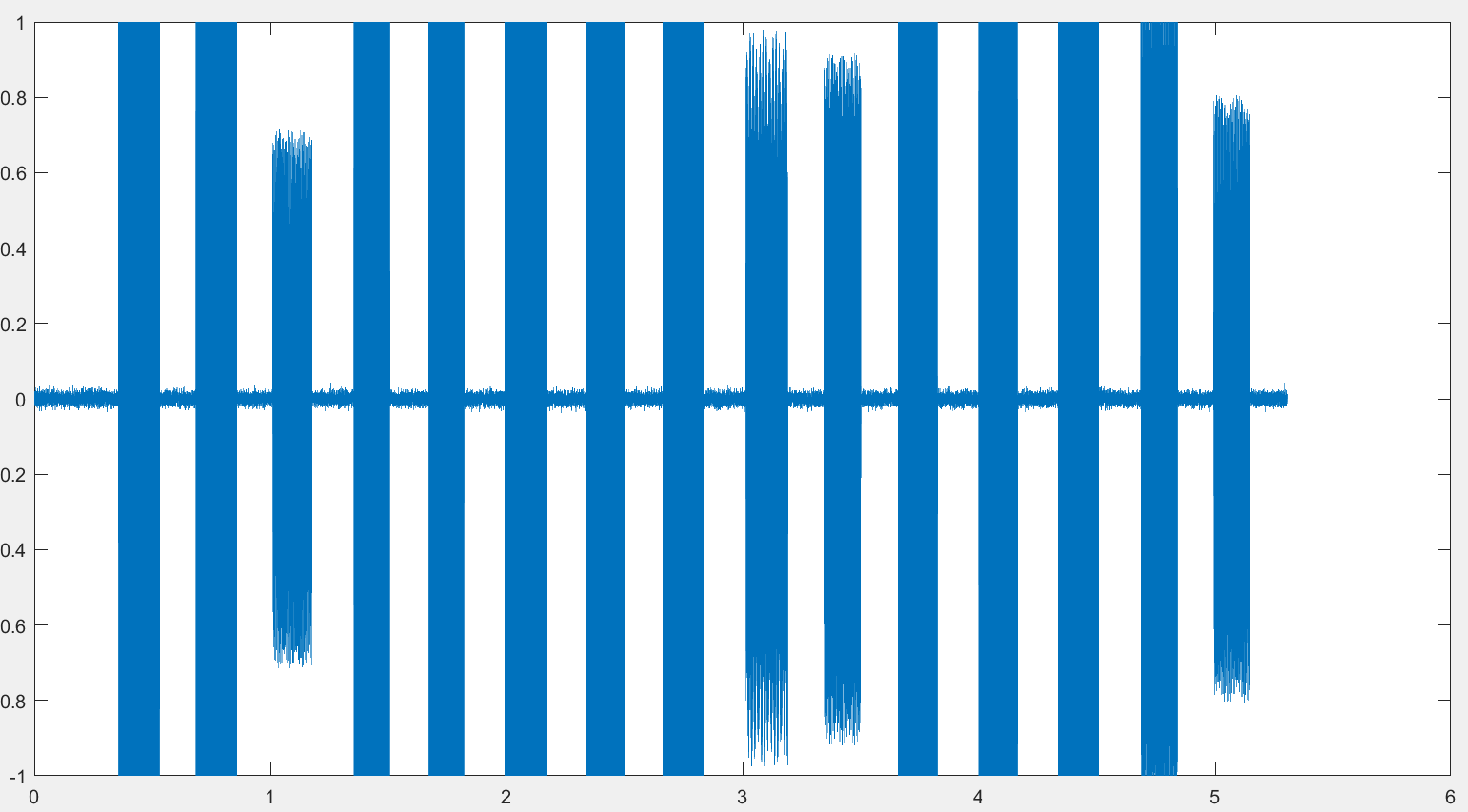
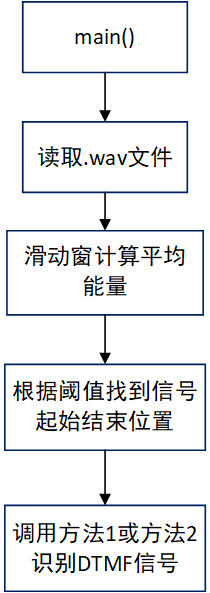
下图为一串DTMF信号的时域图像,可以看到其中包含了15个DTMF信号,我们要做的工作是确定每一个信号的起始于结束位置,直接使用强度值进行判断存在较大的误差,因此选择滑动窗取平均的方式。程序中选择滑动窗大小为64,计算信号每个点对应的滑动窗内的平均能量,并与阈值作比较,从而确定每一个信号的起始结束位置。之后将每一段信号采用上述的两种方法进行信号判断
- 程序框图
2.两种算法的结果与复杂度比较
实验结果:
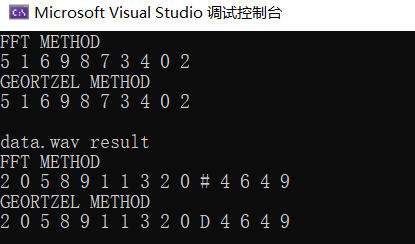
复杂度分析:
FFT方法采用DFT计算了所有的频点信息,时间复杂度为$O(nlogn)$,寻找峰值的复杂度为O(n),总的时间复杂度为$O(nlogn) + O(n)$
Goertzel方法只计算特定的8个频点,并采用差分方程的形式递推计算,时间复杂度为O(n)
FFT方法需要存储所有的频域信息,空间复杂度为$O(n)$, Goertzel方法在递推过程中只需要V[i-1]、V[i-2]这两个状态, 空间复杂度为$O(1)$