并查集

并查集

并查集可以说在算法中应用很广泛，最主要用来判断图的连通性的问题。之前做的题很少包含按秩合并，最多就是按照两个连通分量的大小进行合并。今天第一次碰到了按照秩进行合并的并查集问题，leetcode 399 除法求值，描述如下：

给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。

另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。

输入：equations = [[“a”,”b”],[“b”,”c”]], values = [2.0,3.0], queries = [[“a”,”c”],[“b”,”a”],[“a”,”e”],[“a”,”a”],[“x”,”x”]]
输出：[6.00000,0.50000,-1.00000,1.00000,-1.00000]

1.深度优先搜索

因为数据规模不大，a / b = 2，可以表示为a到b有一条权值为2的边，b到a有一条权值为0.5的边，因此对于每一个查询，可以采用深度优先搜索的方式进行查找，记录路径与当前的乘积，时间复杂度为O(n)。

2.并查集方法

• a / b = 2.0 说明a 与 b在一个集合中，a = 2b

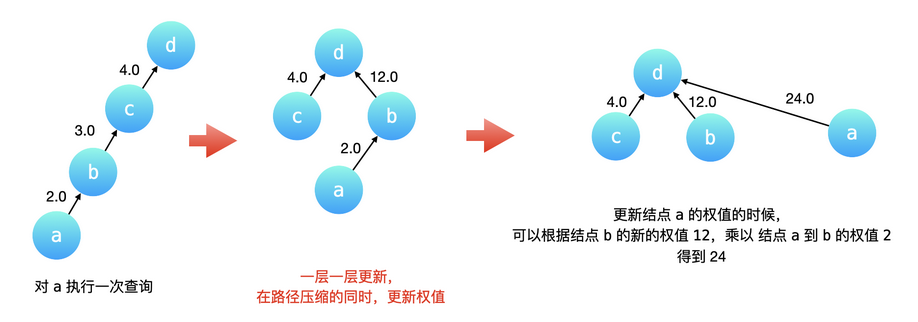
• 带路径压缩的查询
  $$
  w[x] = \frac{v[x]}{v[father} \
  w[x] = \frac{v[x]}{v[fa[x]]} * \frac{v[fa[x]]}{v[father]} \
  w[x] = w[x] * w[fa[x]]
  $$
  

• 按秩合并

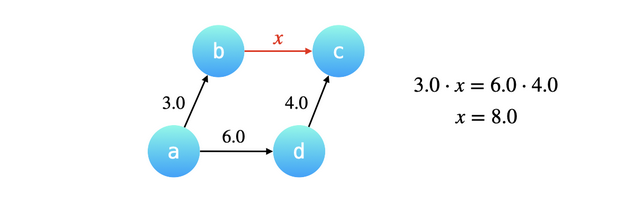
  合并两个节点的父亲，要更新两个父亲之间的权值。
  $$
  w[fx] = \frac{v[fx]}{v[fy]} \
  w[fx] = \frac{v[x]}{w[x]} / \frac{v[y]}{w[y]} \
  $$

class UnionFind {
private:
    int n;
    vector<int> fa;
    vector<double> w;
public:
    UnionFind(int _n) : n(_n), fa(n, 0), w(n, 1.0) {
        for (int i = 0; i < n; ++i) fa[i] = i;
    }

    int find(int x) {
        if (x != fa[x]) {
            int father = find(fa[x]);
            w[x] *= w[fa[x]];
            fa[x] = father;
        }
        return fa[x];
    }

    void unite(int x, int y, double weight) {
        int fx = find(x), fy = find(y);
        if (fx == fy) return;
        fa[fx] = fy;
        w[fx] = weight * w[y] / w[x];
    }
    
    double isConnected(int x, int y) {
        int fx = find(x), fy = find(y);
        if (fx == fy) {
            return w[x] / w[y];
        } else {
            return -1;
        }
    }
};

class Solution {
public:
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        unordered_map<string, int> mp;
        int idx = 0, n = equations.size();
        UnionFind uf(2 * n);
        for (int i = 0; i < n; ++i) {
            string s = equations[i][0], t = equations[i][1];
            if (!mp.count(s)) mp[s] = idx++;
            if (!mp.count(t)) mp[t] = idx++;
            uf.unite(mp[s], mp[t], values[i]);
        }
        vector<double> ans;
        for (auto p : queries) {
            if (!mp.count(p[0]) || !mp.count(p[1])) ans.push_back(-1.0);
            else ans.push_back(uf.isConnected(mp[p[0]], mp[p[1]]));
        }
        return ans;
    }
};