凸优化
leetcode 1515 服务中心的最佳位置
一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标,并希望能够以此为依据为新的服务中心选址:使服务中心 到所有客户的欧几里得距离的总和最小 。给你一个数组 positions ,其中 positions[i] = [xi, yi] 表示第 i 个客户在二维地图上的位置,返回到所有客户的 欧几里得距离的最小总和
该问题本质上优化的函数如下:
$$
f(x_c, y_c) = \sum\limits_{i = 0}^{n - 1}\sqrt{(x_c - x_i)^2 + (y_c - y_i)^2}
$$
其中$(x_c, y_c)$为服务器中心的位置,其可以使$f(x_c, y_c)$取得最小值。该函数是凸函数,凸优化问题的局部最优解就是全局最优解。
1.凸集
$C$是凸集,如果对于任意的$x,y\in C$和任意的$\theta \in \mathbb{R}$且满足$0 \le \theta \le 1$时,$\theta x + (1 - \theta) y$恒成立。
2.凸函数
2.1 凸函数定义
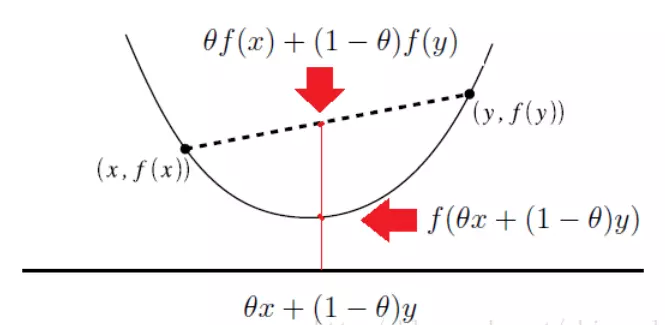
定义在$\mathbb{R}^n \rightarrow \mathbb{R}$上的函数$f$是凸函数, 当且仅当它的定义域$\mathbb{D}(f)$是一个凸集,且对于任意的$x, y \in \mathbb{D}$和$ 0 \le \theta \le 1$, $f(\theta x + (1 - \theta)y) \le \theta f(x) + (1 - \theta)f(y)$恒成立。
2.2 凸函数的一阶充要条件
假设定义在$\mathbb{R}^n \rightarrow \mathbb{R}$上的函数$f$可微, 即对于所有的$x \in \mathbb{D}(f)$,梯度$\nabla f(x)$均存在,则函数$f$是凸函数当且仅当函数定义域$\mathbb{D}(f)$是一个凸集合,且对于所有$x, y \in \mathbb{D}(f)$均满足:
$$
f(y) \ge f(x) + \nabla f(x)^T(y - x)
$$
2.3 凸函数的二阶充要条件
记凸函数$f$的一阶导数和二阶导数分别为$g$和$H$
$$
\nabla f = \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2}\\ \vdots \\ \frac{\partial f}{\partial x_n} \end{bmatrix} \quad
H = \nabla^2f = \begin{bmatrix} \frac{\partial^2f}{\partial x_1^2} & \frac{\partial^2f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2f}{\partial x_1 \partial x_n} \\ \frac{\partial^2f}{\partial x_2 \partial x_1} & \frac{\partial^2f}{\partial x_2^2} & \cdots & \frac{\partial^2f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2f}{\partial x_n \partial x_1} & \frac{\partial^2df}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2f}{\partial x_n^2} \end{bmatrix}
$$
$f$在$x_k$处的二阶泰勒展开为
$$
f(x) = f(x_k) + \nabla f^T (x - x_k) + \frac{1}{2!}(x - x_k)H(x_k)(x - x_k) + o^n
$$
假设定义在$\mathbb{R}^n \rightarrow \mathbb{R}$上的函数$f$二阶可微, 即对于所有的$x \in \mathbb{D}(f)$,海森矩阵$\nabla^2 f(x)$均存在,则函数$f$是凸函数当且仅当函数定义域$\mathbb{D}(f)$是一个凸集合,且对于所有$x, y \in \mathbb{D}(f)$均满足$H$为半正定矩阵。
3.凸优化
可以证明本题优化的函数$f$为$\mathbb{R}^2$的上凸函数。
梯度下降
模拟退火
爬山算法
三分搜索
3.1 梯度下降
梯度下降算法,梯度下降是机器学习中常用的一种求局部最小值的算法,对于给定点$(x, y)$,它的梯度方向是函数值上升最快的方向,因此负梯度为函数值下降的最快的方向,$-\nabla f = (-\frac{\partial f}{\partial x}, -\frac{\partial f}{\partial y})$,我们从一个初始点$(x_{start}, y_{start})$开始迭代, 每次令
$$
x \prime = x - \alpha \cdot \frac{\partial f}{\partial x} \\
y \prime = y - \alpha \cdot \frac{\partial f}{\partial y}
$$
初始点$(x_{start}, y_{start})=(\frac{\sum\limits_{i =0}^{n-1}x_i}{n},\frac{\sum\limits_{i =0}^{n-1}y_i}{n})$
学习率$\alpha = 1$
学习率衰减$\eta = 0.001$
当$(x \prime, y\prime)$与$(x, y)$的距离小于$10^{-7}$时结束迭代。
1 | class Solution { |
整体写下来,尝试了很多次,初始值与学习率与学习率衰减的设置都会很大程度上影响是否能够收敛到最优值。该算法对初始化参数设置的依赖较大。
3.2 爬山算法
如果给定的凸函数很难求导,我们注意到负梯度方向,$\nabla f = -\frac{\partial f}{\partial x}(1, 0) -\frac{\partial f}{\partial y}(0, 1)$,开始我们选择一个步长,表示每次移动的距离。如果我们当前在位置$(x, y)$,我们一次枚举四个方向,判断其函数值是否更小,如果更小则进行移动,否则说明我们的步长过大,直接跳过了最优值点,调整步长为原来的一半,直到步长小于给定的阈值。
1 | class Solution { |