跳表 | TYS的博客

跳表(Probabilistic Alternative to Balanced Trees)

跳跃表是一种有序的数据结构，它通过在每个节点中维持多个指向其他节点的指针，从而达到快速访问节点的目的。跳表的期望空间复杂度为$O(n)$，跳表的查询，插入和删除操作的期望时间复杂度都为$O(logn)$。

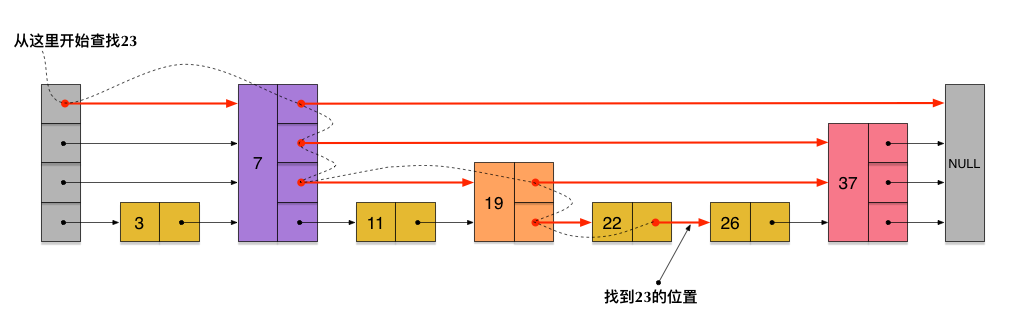
链表加多级索引的结构就是跳表。跳表的每一层都是一个有序链表，每层位于第i层的节点有p的概率出现在第i+1层，p为常数。

复杂度证明

空间复杂度

第一层的期望值为$n$, 第二层的期望值为$np$, 第三层的期望值为$np^2$，因此空间复杂度的期望值为$\sum\limits_{i = 0}^{+\infty}np^i=\frac{n}{1 - p}$。因为p为常数，因此跳表期望的空间复杂度为$O(n)$。

时间复杂度

跳表最后一层节点的个数为$\frac{1}{p}$，因为再上一层的期望值为1(无意义)。因此层数m为
$$
np^{m - 1}=\frac{1}{p} \\
(\frac{1}{p})^m=n \\
m = \log_{\frac{1}{p}}n
$$
跳表skiplist的平均查找长度，查找长度指的是查找路径上跨越的跳数，查找过程中的比较次数等于查找长度加1（每比较一次要么向下一层，要么到本层的右侧节点)。每个节点在进行插入的时候，它的层数是由随机函数randomLevel()计算出来的，随机的计算不依赖于其它的节点，每个节点是独立同分布的，每次插入过程都是完全独立的。

为了计算查找长度，我们将逆向还原查找过程，从右下方第一层最后到达的那个节点开始，沿着查找路径向左，向上回溯。假设当回溯到某个节点的时候，它才被插入，这虽然相当于改变了节点的插入顺序，但从统计上不影响整个skiplist的形成结构。

如果某一个节点有上层节点的话，则我们需要向上走，整个查找过程类似楼梯的形状，每个节点第一被访问一定是位于其最顶层。

如果节点x有第i+1，那么我们需要向上走，这种情况概率为p
如果节点没有第i+1层指针，那么我们需要向左走，这种情况的概率为1-p

用C(k)表示向上攀爬k个层级所需要走过的平均查找路径长度，因此有
$$
C(k) = (1 - p)*(C(k) + 1) + p * (C(k - 1) + 1) \\
C(k) = \frac{1}{p} + C(k - 1) \\
C(k) = \frac{k}{p}
$$
n个节点跳表的层数为$\log_{\frac{1}{p}}n$，因此所需时间为$\frac{\log_{\frac{1}{p}}n}{p}$，即平均时间复杂度为$O(\log n)$

代码实现

数据结构SkipListNode，skiplist真正有数据只有下面一层的数据节点，每个节点的后继就是level[0],

struct SkipListNode {
	int val;
	vector<SkipListNode *> level;
	SkipListNode (int _val, int sz=32) : val(_val), level(sz, nullptr) {}
};

class Skiplist {
private:
    SkipListNode *head, *tail;
    int level, length;
public:
	static constexpr int MAXL = 32;
    static constexpr int P = 4;
    static constexpr int S = 0xFFFF;
    static constexpr int PS = S / 4;

    Skiplist() {
        level = length = 0;
        tail = new SkipListNode(INT_MAX, 0);
        head = new SkipListNode(INT_MAX);
        for (int i = 0; i < MAXL; ++i) { 
        	head->level[i] = tail;
        }
    }

    SkipListNode* find(int val) {
        SkipListNode *p = head;
        for (int i = level - 1; i >= 0; --i) {
            while (p->level[i] && p->level[i]->val < val) {
                p = p->level[i];
            }
        }
        p = p->level[0];
        return p;
    }
    
    bool search(int target) {
        SkipListNode *p = find(target);
        return p->val == target;
    }
    
    void add(int val) {
        vector<SkipListNode *> update(MAXL);
        SkipListNode *p = head;
        for (int i = level - 1; i >= 0; --i) {
            while (p->level[i] && p->level[i]->val < val) {
                p = p->level[i];
            }
            update[i] = p;
        }
        int lv = randomLevel();
        if (lv > level) {
            lv = ++level;
            update[lv - 1] = head; 
        }
        SkipListNode *newNode = new SkipListNode(val, lv);
        for (int i = lv - 1; i >= 0; --i) {
            p = update[i];
            newNode->level[i] = p->level[i];
            p->level[i] = newNode;
        }
        ++length;
    }
    
    bool erase(int val) {
        vector<SkipListNode *> update(MAXL + 1);
        SkipListNode *p = head;
        for (int i = level - 1; i >= 0; --i) {
            while (p->level[i] && p->level[i]->val < val) {
                p = p->level[i];
            }
            update[i] = p;
        }
        p = p->level[0];
        if (p->val != val) return false;
        for (int i = 0; i < level; ++i) {
            if (update[i]->level[i] != p) {
                break;
            }
            update[i]->level[i] = p->level[i];
        }
        while (level > 0 && head->level[level - 1] == tail) --level;
        --length;
        return true;
    }

    int randomLevel() {
        int lv = 1;
        while (lv < MAXL && (rand() & S) < PS) ++lv;
        return lv;
    }
};

参考文章

http://zhangtielei.com/posts/blog-redis-skiplist.html

ftp://ftp.cs.umd.edu/pub/skipLists/skiplists.pdf

https://oi-wiki.org/ds/skiplist/#_4