凸包

凸包

二维凸包， 凸多边形是指所有内角大小都在$[0, \pi]$范围内的简单多边形。在平面上能包含所有给定点的最小凸多边形叫做凸包。

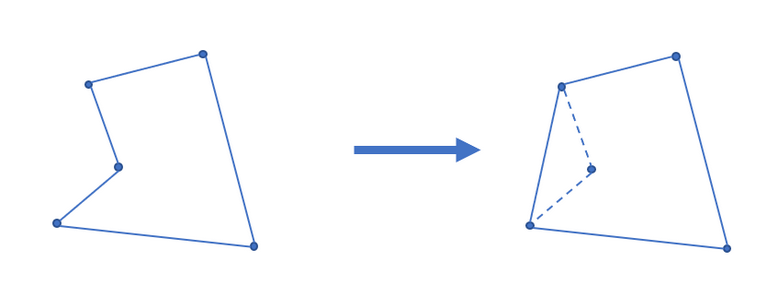
Andrew算法

$\quad\quad$首先将点集按照x坐标(第一关键字)，y坐标进行升序排列。显然排序后最小的元素和最大的元素一定在凸包上。他们之间的部分可以分成上下两条链分别求解。求下链时只要从小到大遍历排序后的点列，求上链从大到小遍历即可。

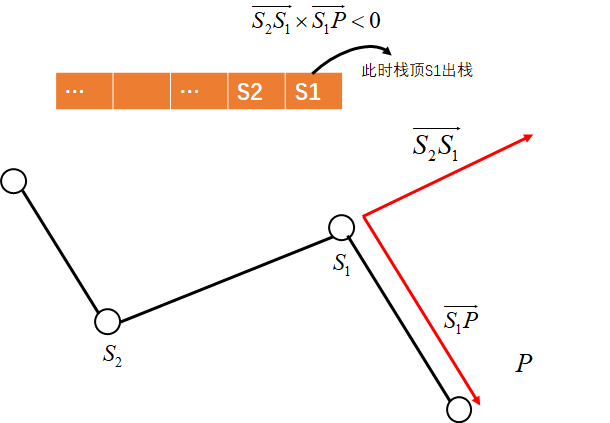
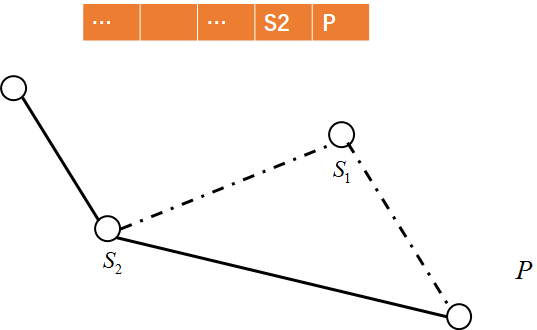
$\quad\quad$在凸包上，我们从一个点出发逆时针走，轨迹总是左拐的，如果出现右拐，则说明该段不在凸包上。采用栈来记录轨迹上已经走过的点，如果即将入栈的点$P$和栈顶点$S_1$构成的向量方向相较$S_2, S_1$构成向量的方向向右旋转，即叉积$\vec{S_2S_1} \times\vec{S_1P} < 0$，则弹出栈顶，直到$\vec{S_2S_1} \times\vec{S_1P} \geq 0$或栈内仅包含一个元素。

代码实现

struct Point {
    int x, y;
    Point(int _x, int _y) : x(_x), y(_y) {}
    
    bool operator < (const Point& rhs) const {
        return x == rhs.x ? y < rhs.y : x < rhs.x;
    }
    
    Point operator - (const Point& rhs) {
        Point ret(0, 0);
        ret.x = x - rhs.x;
        ret.y = y - rhs.y;
        return ret;
    }
    
    int operator ^ (const Point& rhs) {
        return x * rhs.y - y * rhs.x; 
    }
};


class Solution {
public:
    vector<vector<int>> outerTrees(vector<vector<int>>& points) {
        vector<Point> arr;
        int n = points.size();
        for (int i = 0; i < n; ++i) {
            arr.push_back({points[i][0], points[i][1]});
        }
        sort(arr.begin(), arr.end());
        int tp = 0;
        vector<bool> used(n, 0);
        vector<int> st(n + 5);
        for (int i = 0; i < n; ++i) {
            while (tp >= 2 && ((arr[st[tp]] - arr[st[tp - 1]]) ^ (arr[i] - arr[st[tp]])) < 0) {
                used[st[tp--]] = false;
            }
            st[++tp] = i;
            used[i] = true;
        }
        used[0] = false;
        for (int i = n - 1; i >= 0; --i) {
            if (used[i]) continue;
            while (tp >= 2 && ((arr[st[tp]] - arr[st[tp - 1]]) ^ (arr[i] - arr[st[tp]])) < 0) {
                used[st[tp--]] = false;
            }
            st[++tp] = i;
            used[i] = true;
        }
        vector<vector<int>> ret;
        for (int i = 1; i < tp; ++i) {
           ret.push_back({arr[st[i]].x, arr[st[i]].y});
        }
        return ret;
    }
};

复杂度分析

• 时间复杂度，排序$O(n\log n)$，上下链求解$O(2n)$
• 空间复杂度，栈的最大深度为O(n)