TYS的博客

算法小白努力学习中

0%

发表于 更新于

RetinaNet

https://zhuanlan.zhihu.com/p/346198300

什么是anchor

https://zhuanlan.zhihu.com/p/55824651

Head模块

路径mmdetection/mmdet/models/dense_heads/retina_head.py

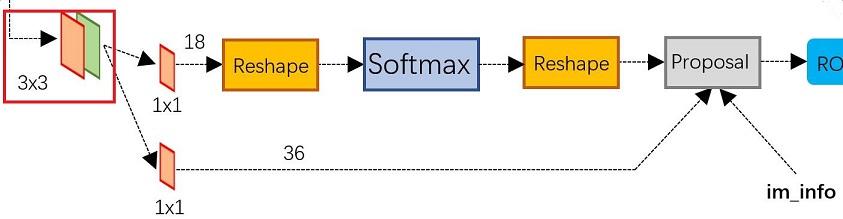
head包含两个子网络 分类与锚框回归分支，两个分支不共享权重，但分支内五个FPN输出特征图权重是共享的。head中的卷积网络为五层，前四层的通道数均为256，最后一层的通道数量 分类为self.num_anchors * self.cls_out_channels，回归为self.num_anchors * 4

1
2
3
4
if self.use_sigmoid_cls:
	self.cls_out_channels = num_classes
else:
    self.cls_out_channels = num_classes + 1

mmcv.cnn.conv_module包含了卷积、norm、activate三个层。

BBox Assigner

RetinaNet属于anchor-based算法，在bbox分配前需要得到特征图每个位置的anchor列表

参数配置定义

1
2
3
4
5
6
7
8
9
10
anchor_generator=dict(
    type='AnchorGenerator',
    # anchor基准大小
    octave_base_scale=4,
    # 每个特征图anchor有三个尺度 2 ** 0、 2 **(1 / 3) = 1.2599、2 ** (2 / 3) =  1.5874
    scales_per_octave=3,
    # 每个特征图anchor有三种宽高比
    ratios=[0.5, 1.0, 2.0],
    # 特征图对于原图的stride
    strides=[8, 16, 32, 64, 128]),

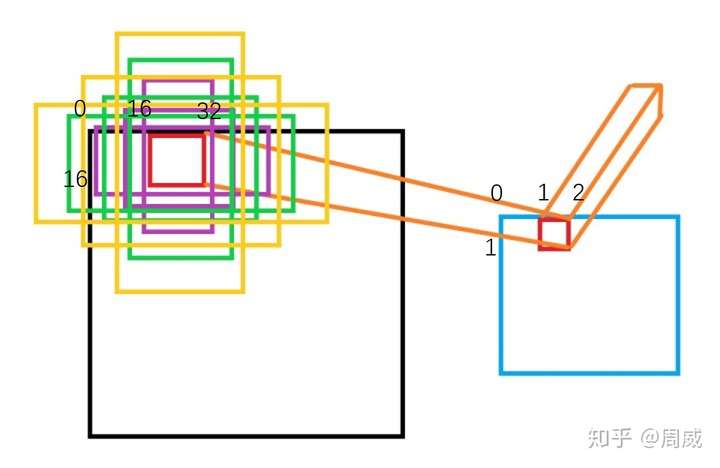
生成anchor_generator对象，对于生成的9个anchor，组内的大小为octave_base_scale * strides在乘上相应的尺度因子。x坐标从左往右递增，y坐标从上往下递增，最左上方可见像素的坐标是（0，0）

image-20211001183443297

Anchor Generator

代码位置mmdet/core/anchor/anchor_generator.py

核心函数gen_single_level_base_anchors

1
2
3
4
5
def gen_single_level_base_anchors(self,
                                  base_size,
                                  scales,  # 尺度因子 这里包含了octave_base_scale的系数
                                  ratios, # 高宽比
                                  center=None):

生成9个anchor 分成三组，每组内的ratio高宽比相同。

_meshgrid函数快速根据一维x，y坐标生成二维的索引坐标

1
2
3
4
5
6
7
 x = torch.tensor(np.array(range(2)))
 y = x.clone()
 xx = x.repeat(y.shape[0])
 yy = y.view(-1, 1).repeat(1, x.shape[0]).view(-1)
# xx tensor([0, 1, 0, 1])
# yy tensor([0, 0, 1, 1])
 shifts = torch.stack([shift_xx, shift_yy, shift_xx, shift_yy], dim=-1) 对第最后一个维度进行拼接

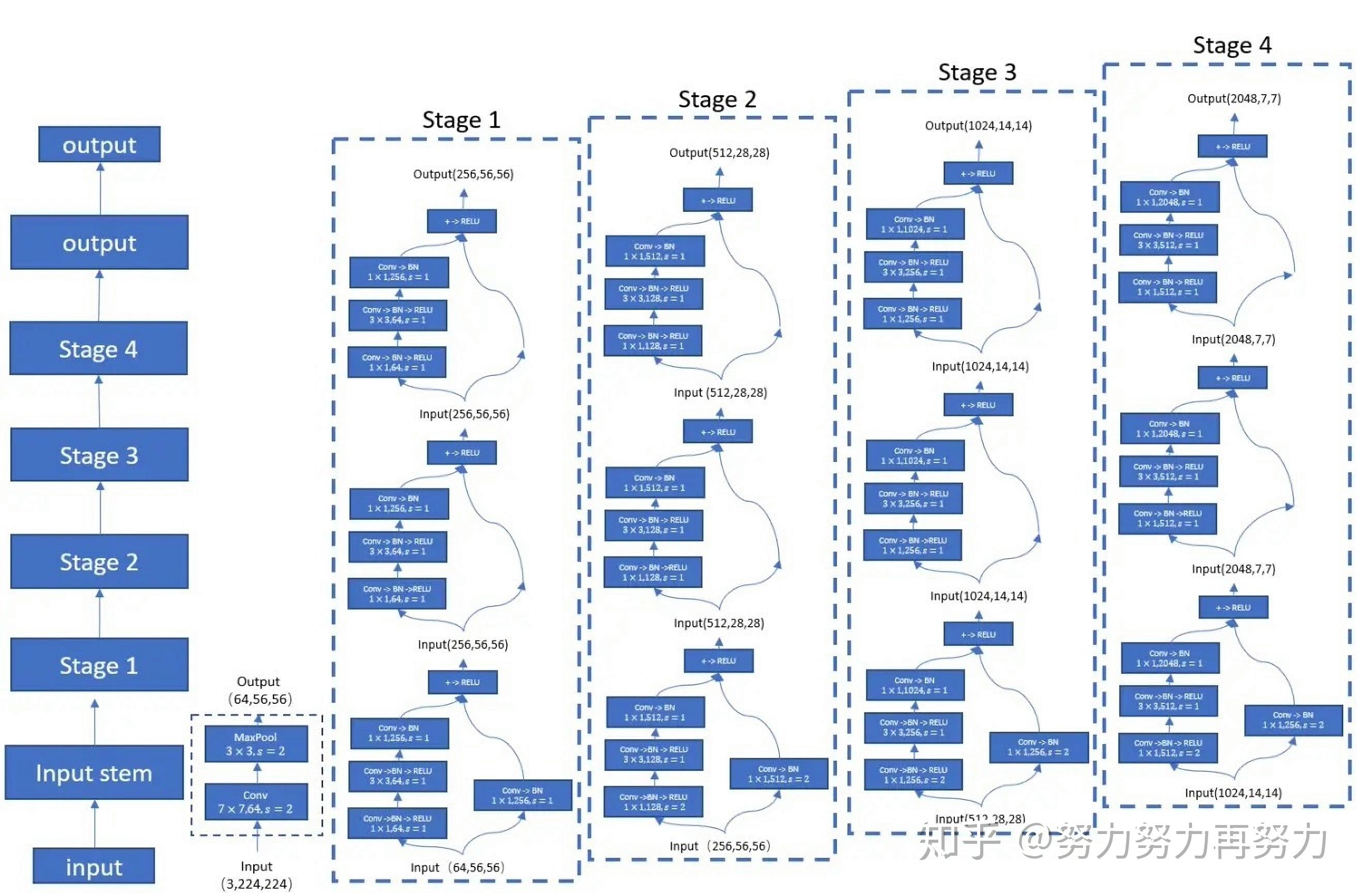
mmdetection中的Retinanet类

在mmdetection中并未对Retinanet做特殊实现，只是用参数初始化了父类SingleStageDetector ，实现文件为mmdet/models/detectors/single_stage.py

1
2
3
4
5
6
7
8
9
10
11
class RetinaNet(SingleStageDetector):
        def __init__(self,
                 backbone,
                 neck,
                 bbox_head,
                 train_cfg=None,
                 test_cfg=None,
                 pretrained=None,
                 init_cfg=None):
        super(RetinaNet, self).__init__(backbone, neck, bbox_head, train_cfg,
                                        test_cfg, pretrained, init_cfg)

发表于 更新于

目标检测中常见的网络结构

FCN 网络

Fully Convolutional Networks for Semantic Segmentation，深度学习在图像分割的代表作，FCN中所有层都是卷积层，故称全卷积网络。

https://zhuanlan.zhihu.com/p/31428783

CNN语义分割基本套路

  • 降采样，上采样，裁减。convlution + deconvlution/ resize
  • 多尺度特征融合：特征点逐点相加/特征channel维度拼接
  • 获得像素级别的segement map 对每一个像素点进行类别判断。

FPN 网络

https://zhuanlan.zhihu.com/p/92005927

具有侧向连接（lateral connections）的网络结构，构建不同尺寸具有高级语义信息的特征图。

融合低分辨率具有较强语义信息的特征图、高分辨率语义信息较弱，但空间信息丰富的特征图。

preview

RPN网络

https://zhuanlan.zhihu.com/p/31426458

Faster RCNN使用RPN网络生成检测框，能极大提升检测框的生成速度。

preview

anchor定义, 特征图上的每个点，对应原图像上的一块区域。

img

定义anchor $A = (A_x, A_y, A_w, A_h)$，$GT = (G_x, G_y, G_w, G_h)$，寻找一种变换$F(A) = G$，该变换为平移与缩放
$$
G_x = x_a + w_a * d_x \
G_y = y_a + h_a * d_y \
G_w = w_a * e^{d_w} \
G_h = h_a * e^{d_h}
$$

当A与GT相差较小时，认为该变换参数是可以采用线性回归来建模$d_* = W^T * \phi$，其中$\phi$是特征图输出的特征向量

positive anchor与ground truth变换之间的平移量$t_x, t_y$，尺度因子$t_w, t_h$如下：
$$
t_x = (x - x_a) / w_a \
t_y = (y - y_a) / h_a \
t_w = log(w / w_a) \
t_h = log(h / h_a)
$$
对于回归分支，输入的是CNN特征，监督变量是anchor与GT的差距$t_x, t_y, t_w, t_h$，训练损失函数
$$
Loss = \sum_i^N|t_^i - W_^T * \phi(A^i)| + \lambda||W_*||
$$
https://mp.weixin.qq.com/s/IJUMCOBhgXHv7VC1YT4q_g

https://cloud.tencent.com/developer/article/1441555

ResNet

残差学习网络

https://zhuanlan.zhihu.com/p/79378841

preview

preview

z

发表于 更新于

题目

https://www.luogu.com.cn/problem/P3865

给定一个长度为N的数列和M次询问，求出每一次询问的区间内数字最大值。

st

令f[i][j]表示区间$[i, i + 2^j - 1]$的最大值。根据倍增的思想，可以写出状态转移方程$f[i][j] = max(f[i][j - 1], f[i + 2^{j - 1}][j - 1])$

因此对于每个询问[l, r]，我们将其分为两部分$[l, l + 2^s - 1], [r - 2^s + 1, r]$，其中$s = log_2(r - l + 1)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
static constexpr int MAXN = 1e5 + 5;
int f[MAXN][21];
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
	#ifndef ONLINE_JUDGE
		freopen("input.txt", "r", stdin);
		freopen("output.txt", "w", stdout);
	#endif
    int n, m, l, r, s;
    cin >> n >> m;
    vector<int> arr(n, 0);
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
        f[i][0] = arr[i];
    }    
    for (int j = 1; j <= 20; j++) {
        for (int i = 0; i + (1 << (j - 1)) < n; i++) {
            f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
        }
    }
    for (int i = 0; i <  m; i++) {
        cin >> l >> r;
        s = log2(r - l + 1);
        cout << max(f[l][s], f[r - (1 << s) + 1][s]) << endl;   
    }
    return 0;
}

发表于 更新于
点在多边形内部

射线法，从判断点向上做一条射线，当与多边形交点个数为奇数个时，则点在多边形内部。

边界条件(点在顶点上，点在边上，通过叉积等于0与点积小于等于0来判断）

边界条件，凸顶点判断一次，凹顶点判断两次

边界条件，当连线与边重叠时，不进行判断，点一定在多边形外部。

image-20210521204309172.png

1
((c.x >= a.x && c.x < b.x) || (c.x >= b.x && c.x < a.x))

image-20210521204412305.png

image-20210521204008259.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include<bits/stdc++.h>
using namespace std;
using LL = long long;

struct Point {
public:
    int x, y;

    Point(int _x, int _y) : x(_x), y(_y) {}

    Point operator - (const Point& rhs) {
        return {x - rhs.x, y - rhs.y};
    }
};

int dot(const Point& a, const Point& b) {
    return a.x * b.x + a.y * b.y;
}

int cross(const Point& a, const Point& b) {
    return a.x * b.y - b.x * a.y;
}

vector<Point> arr;
bool in(Point c) {
    int n = arr.size();
    int ans = 0;
    for (int i = 0, j = n - 1; i < n; j = i++) {
        Point a = arr[j], b = arr[i];
        if (dot(c - a, c - b) <= 0 && cross(c - a, c - b) == 0) return 0;
        if (((c.x >= a.x && c.x < b.x) || (c.x >= b.x && c.x < a.x)) && c.y < a.y + 1.0 * (b.y - a.y) / (b.x - a.x) * (c.x - a.x)) {
            ans = !ans;
        }
    }
    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    #ifndef ONLINE_JUDGE
        freopen("input.txt", "r", stdin);
        freopen("output.txt", "w", stdout);
    #endif
    int n, q, x, y;
    cin >> n;
    for (int i = 0; i < n; ++i) {
        cin >> x >> y;
        arr.push_back({x, y});
    } 
    cin >> q;
    int ans = 0;
    for (int i = 0; i < q; ++i) {
        cin >> x >> y;
        if (in({x, y})) ++ans;
    }
    cout << ans << endl;
    return 0;
}

发表于 更新于

关于素数的一些方法

假设N为1e5，对1到N中所有的数做质因子分解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
static constexpr int N = 1e5 + 5;
unordered_map<int, int> prime[N];
bool isp[N];
{
    memset(isp, true, sizeof(isp));
    for (int i = 2; i < N; ++i) {
        if (isp[i]) {
            for (int j = i; j < N; j += i) {
                int cur = j, cnt = 0;
                while (cur % i == 0) {
                    cur /= i;
                    ++cnt;
                }
                prime[j][i] = cnt;
                isp[j] = false;
            }
        }
    }
}

找到1到N中所有数的因数

1
2
3
4
5
6
vector<int> fact[N];
for (int i = 1; i < N; ++i) {
    for (int j = 2 * i; j < N; j += i) {
        fact[j].push_back(i);
    }
}

找到[1:m]中满足$gcd(n, p) = x$的$p$的数量。

$$
gcd(n, p) = x \\
n = a \cdot x, p = b \cdot x \\
gcd(a, b) = 1
$$
找到[1:b]中gcd(a, b) = 1中数字的数量，计算[1:b]中gcd(a, b) != 1的数量, prime[a]为a的质因数分解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int find(int a, int b) {
    int ans = 0;
    vector<int> arr;
    for (auto it : prime[a]) {
        arr.push_back(it.first);
    }
    int sz = arr.size();
    for (int i = 1; i < (1 << sz); ++i) {
        int mul = 1, sign = -1;
        for (int j = 0; j < sz; ++j) {
            if (i >> j & 1) {
                mul *= arr[j];
                sign *= -1;
            }
        }
        ans += sign * b / mul;
    }
    return b - ans;
}

例题：https://codeforces.com/problemset/problem/1139/D

其中cnt为1到m中gcd(p, x) = y的p的数量。
$$
f[x] = 1 + \frac{cnt}{m}f[y] + \frac{\frac{m}{x}}{m}f[x]
$$

发表于 更新于

组合数学DP

一个挺有意思的题目

https://cses.fi/problemset/task/1717

There are n children at a Christmas party, and each of them has brought a gift. The idea is that everybody will get a gift brought by someone else. In how many ways can the gifts be distributed?

发表于 更新于

错排公式

错排问题，考虑$n$个元素的排列，若一个排列中所有的元素都不在自己原来的位置上，那么这样的排列就称为原排列的一个错排。记作$n$个元素的错排数为$D(n)$。

递推公式：

  • 选择书的编号为m，剩下n - 1个位置，假设选择k

  • k放入m的位置 则转化为$D(n - 2)$的错排方案数

  • 第m本书在位置k不动，此时k不能放在第m个位置，其他n - 2本书也不在自己原本的位置，等价于求$n - 1$个数的错排

$$
D(n) = (n - 1) *[D(n- 1) + D(n - 2)]
$$

https://cses.fi/problemset/task/1717

发表于 更新于

Transformer中的Embedding

https://blog.csdn.net/qq_35799003/article/details/84780289

将词汇表中的每个单词进行one-hot编码存在的问题

  • 稀疏向量过大，导致模型无法训练。向量间缺少距离的度量。

解决方案采用Embedding，将高纬稀疏向量映射到低维空间，同时保留语义关系。

发表于 更新于

java注解

注解可以被编译器打包进入class文件，是一种用作标注的元数据。

  • 由编译器使用的注解@Override让编译器检查该方法是否正确地实现了覆写。这类注解不会被编译进入.class文件，在编译后就被扔掉了
  • 由工具类处理.class文件使用的注解。
  • 程序运行期能够读取的注解，加载后一直存在于JVM中，例如@PostConstruct方法在调用构造方法后自动被调用。

1.定义注解

java语言使用@interface语法来定义注解(Annotation)

2.使用注解

通常注解如何使用由程序自己决定。

发表于 更新于

wilson定理

正整数n > 1， 则n是一个素数当且仅当$(n - 1)! \equiv -1 (mod\ n)$

如果n为非质数，假设集合A为${1, x_1, x_2,\cdots x_{m - 1}, n - 1}$与n互质。

对于任意$x_i$，则$x_i \cdot A$集合为${x_i,\ x_i\cdot x_1,\ x_i \cdot x_2,\ \cdots,\ x_i \cdot x_{m - 1},\ x_i \cdot (n - 1)}$, 对于其中$x_i\cdot A$中任意一个元素其膜n的值互不相同，且为集合A中的元素，因此存在$x_i * x_j \equiv 1 (mod\ n)$，因为1和n - 1模n逆元为其本身，$x_i$的逆元为$x_j$
$$
(1\times x_1 \times x_2 \times \cdots x_m \times n - 1) \cdot (1\times x_1 \times x_2 \times \cdots x_m \times n - 1) \equiv (1 * 1) \times (x_i * x_j) \cdots \times ((n - 1) * (n - 1)) \equiv 1 (mod \ n) \\
令(1\times x_1 \times x_2 \times \cdots x_m \times n - 1) = y \\
y^2\equiv 1 (mod\ n)\\
y \equiv 1 (mod\ n)\ 或\ y \equiv n - 1 (mod\ n)
$$

$$
x_i*x_j \equiv x_i * x_k (mod\ n) \\
x_i * (x_j - x_k) \equiv 0 (mod\ n) \\
(x_j - x_k) \equiv 0 (mod\ n) \\
x_j = x_k
$$