TYS的博客

欧拉函数

发表于 2021-03-07 更新于 2021-09-10

欧拉函数

欧拉函数是小于或等于n的正整数中与n互质的数目，$\phi(1) = 1$。

通式：
$$
\phi(x)= x \mathop{\Pi}\limits_{i = 1}^{n}(1 - \frac{1}{p_i})
$$
若n是质数的p的k次幂，$\phi(n) = p^k - p^{k - 1}$，因为除了p的倍数$p * (1,2\dots p^{k - 1})$以外，其他数均与n互质。

线性筛，每个合数通过其最小的质因数筛掉。

凸包

发表于 2021-03-01 更新于 2021-09-10

凸包

二维凸包，凸多边形是指所有内角大小都在$[0, \pi]$范围内的简单多边形。在平面上能包含所有给定点的最小凸多边形叫做凸包。

Andrew算法

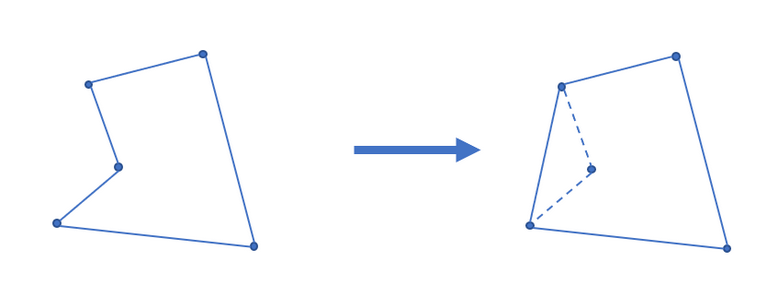
$\quad\quad$首先将点集按照x坐标(第一关键字)，y坐标进行升序排列。显然排序后最小的元素和最大的元素一定在凸包上。他们之间的部分可以分成上下两条链分别求解。求下链时只要从小到大遍历排序后的点列，求上链从大到小遍历即可。

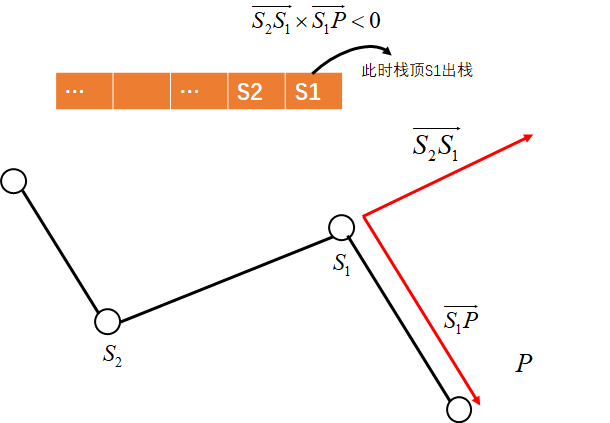
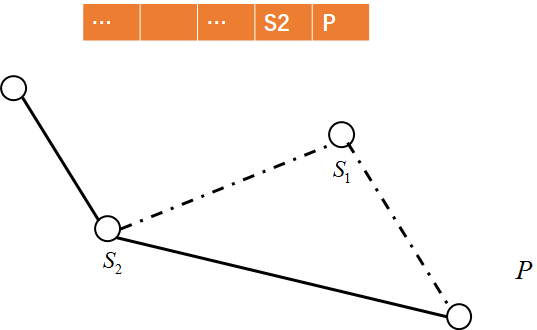
$\quad\quad$在凸包上，我们从一个点出发逆时针走，轨迹总是左拐的，如果出现右拐，则说明该段不在凸包上。采用栈来记录轨迹上已经走过的点，如果即将入栈的点$P$和栈顶点$S_1$构成的向量方向相较$S_2, S_1$构成向量的方向向右旋转，即叉积$\vec{S_2S_1} \times\vec{S_1P} < 0$，则弹出栈顶，直到$\vec{S_2S_1} \times\vec{S_1P} \geq 0$或栈内仅包含一个元素。

代码实现

struct Point {
    int x, y;
    Point(int _x, int _y) : x(_x), y(_y) {}
    
    bool operator < (const Point& rhs) const {
        return x == rhs.x ? y < rhs.y : x < rhs.x;
    }
    
    Point operator - (const Point& rhs) {
        Point ret(0, 0);
        ret.x = x - rhs.x;
        ret.y = y - rhs.y;
        return ret;
    }
    
    int operator ^ (const Point& rhs) {
        return x * rhs.y - y * rhs.x; 
    }
};


class Solution {
public:
    vector<vector<int>> outerTrees(vector<vector<int>>& points) {
        vector<Point> arr;
        int n = points.size();
        for (int i = 0; i < n; ++i) {
            arr.push_back({points[i][0], points[i][1]});
        }
        sort(arr.begin(), arr.end());
        int tp = 0;
        vector<bool> used(n, 0);
        vector<int> st(n + 5);
        for (int i = 0; i < n; ++i) {
            while (tp >= 2 && ((arr[st[tp]] - arr[st[tp - 1]]) ^ (arr[i] - arr[st[tp]])) < 0) {
                used[st[tp--]] = false;
            }
            st[++tp] = i;
            used[i] = true;
        }
        used[0] = false;
        for (int i = n - 1; i >= 0; --i) {
            if (used[i]) continue;
            while (tp >= 2 && ((arr[st[tp]] - arr[st[tp - 1]]) ^ (arr[i] - arr[st[tp]])) < 0) {
                used[st[tp--]] = false;
            }
            st[++tp] = i;
            used[i] = true;
        }
        vector<vector<int>> ret;
        for (int i = 1; i < tp; ++i) {
           ret.push_back({arr[st[i]].x, arr[st[i]].y});
        }
        return ret;
    }
};

复杂度分析

时间复杂度，排序$O(n\log n)$，上下链求解$O(2n)$
空间复杂度，栈的最大深度为O(n)

跳表

发表于 2021-02-27 更新于 2021-09-10

跳表(Probabilistic Alternative to Balanced Trees)

跳跃表是一种有序的数据结构，它通过在每个节点中维持多个指向其他节点的指针，从而达到快速访问节点的目的。跳表的期望空间复杂度为$O(n)$，跳表的查询，插入和删除操作的期望时间复杂度都为$O(logn)$。

链表加多级索引的结构就是跳表。跳表的每一层都是一个有序链表，每层位于第i层的节点有p的概率出现在第i+1层，p为常数。

复杂度证明

空间复杂度

第一层的期望值为$n$, 第二层的期望值为$np$, 第三层的期望值为$np^2$，因此空间复杂度的期望值为$\sum\limits_{i = 0}^{+\infty}np^i=\frac{n}{1 - p}$。因为p为常数，因此跳表期望的空间复杂度为$O(n)$。

时间复杂度

跳表最后一层节点的个数为$\frac{1}{p}$，因为再上一层的期望值为1(无意义)。因此层数m为
$$
np^{m - 1}=\frac{1}{p} \\
(\frac{1}{p})^m=n \\
m = \log_{\frac{1}{p}}n
$$
跳表skiplist的平均查找长度，查找长度指的是查找路径上跨越的跳数，查找过程中的比较次数等于查找长度加1（每比较一次要么向下一层，要么到本层的右侧节点)。每个节点在进行插入的时候，它的层数是由随机函数randomLevel()计算出来的，随机的计算不依赖于其它的节点，每个节点是独立同分布的，每次插入过程都是完全独立的。

为了计算查找长度，我们将逆向还原查找过程，从右下方第一层最后到达的那个节点开始，沿着查找路径向左，向上回溯。假设当回溯到某个节点的时候，它才被插入，这虽然相当于改变了节点的插入顺序，但从统计上不影响整个skiplist的形成结构。

如果某一个节点有上层节点的话，则我们需要向上走，整个查找过程类似楼梯的形状，每个节点第一被访问一定是位于其最顶层。

如果节点x有第i+1，那么我们需要向上走，这种情况概率为p
如果节点没有第i+1层指针，那么我们需要向左走，这种情况的概率为1-p

用C(k)表示向上攀爬k个层级所需要走过的平均查找路径长度，因此有
$$
C(k) = (1 - p)*(C(k) + 1) + p * (C(k - 1) + 1) \\
C(k) = \frac{1}{p} + C(k - 1) \\
C(k) = \frac{k}{p}
$$
n个节点跳表的层数为$\log_{\frac{1}{p}}n$，因此所需时间为$\frac{\log_{\frac{1}{p}}n}{p}$，即平均时间复杂度为$O(\log n)$

代码实现

数据结构SkipListNode，skiplist真正有数据只有下面一层的数据节点，每个节点的后继就是level[0],

struct SkipListNode {
	int val;
	vector<SkipListNode *> level;
	SkipListNode (int _val, int sz=32) : val(_val), level(sz, nullptr) {}
};

class Skiplist {
private:
    SkipListNode *head, *tail;
    int level, length;
public:
	static constexpr int MAXL = 32;
    static constexpr int P = 4;
    static constexpr int S = 0xFFFF;
    static constexpr int PS = S / 4;

    Skiplist() {
        level = length = 0;
        tail = new SkipListNode(INT_MAX, 0);
        head = new SkipListNode(INT_MAX);
        for (int i = 0; i < MAXL; ++i) { 
        	head->level[i] = tail;
        }
    }

    SkipListNode* find(int val) {
        SkipListNode *p = head;
        for (int i = level - 1; i >= 0; --i) {
            while (p->level[i] && p->level[i]->val < val) {
                p = p->level[i];
            }
        }
        p = p->level[0];
        return p;
    }
    
    bool search(int target) {
        SkipListNode *p = find(target);
        return p->val == target;
    }
    
    void add(int val) {
        vector<SkipListNode *> update(MAXL);
        SkipListNode *p = head;
        for (int i = level - 1; i >= 0; --i) {
            while (p->level[i] && p->level[i]->val < val) {
                p = p->level[i];
            }
            update[i] = p;
        }
        int lv = randomLevel();
        if (lv > level) {
            lv = ++level;
            update[lv - 1] = head; 
        }
        SkipListNode *newNode = new SkipListNode(val, lv);
        for (int i = lv - 1; i >= 0; --i) {
            p = update[i];
            newNode->level[i] = p->level[i];
            p->level[i] = newNode;
        }
        ++length;
    }
    
    bool erase(int val) {
        vector<SkipListNode *> update(MAXL + 1);
        SkipListNode *p = head;
        for (int i = level - 1; i >= 0; --i) {
            while (p->level[i] && p->level[i]->val < val) {
                p = p->level[i];
            }
            update[i] = p;
        }
        p = p->level[0];
        if (p->val != val) return false;
        for (int i = 0; i < level; ++i) {
            if (update[i]->level[i] != p) {
                break;
            }
            update[i]->level[i] = p->level[i];
        }
        while (level > 0 && head->level[level - 1] == tail) --level;
        --length;
        return true;
    }

    int randomLevel() {
        int lv = 1;
        while (lv < MAXL && (rand() & S) < PS) ++lv;
        return lv;
    }
};

参考文章

http://zhangtielei.com/posts/blog-redis-skiplist.html

ftp://ftp.cs.umd.edu/pub/skipLists/skiplists.pdf

https://oi-wiki.org/ds/skiplist/#_4

JAVA反射

发表于 2021-02-24 更新于 2021-09-10

JAVA 反射

反射是为了解决运行期，对某个对象一无所知的情况下，调用其方法，JVM为每一个加载的class创建一个Class类型的实例，并关联起来。

通过Class实例获取class信息的方法称为反射(Reflection)

1. 访问字段

Java的反射API提供的Field类封装了字段的所有信息：
通过Class实例的方法可以获取Field实例：getField()，getFields()，getDeclaredField()，getDeclaredFields()；
通过Field实例可以获取字段信息：getName()，getType()，getModifiers()；
通过Field实例可以读取或设置某个对象的字段，如果存在访问限制，要首先调用setAccessible(true)来访问非public字段。
通过反射读写字段是一种非常规方法，它会破坏对象的封装。****

2.调用方法

3.调用构造方法、获取继承关系

4.动态代理

JAVA_Spring

发表于 2021-02-24 更新于 2021-09-10 分类于 JAVA

IOC(Inversion of Control控制反转)

应用本身不负责依赖对象的创建和维护，依赖对象的创建和维护是由外部容器负责的称为控制反转。

IOC容器管理的对象称为Bean，Bean是由Spring容器初始化，装配及管理的对象。

DI(Dependency Injection依赖注入)

设计模式

发表于 2021-02-22 更新于 2021-09-10

设计模式

设计模式本质上是面向对象设计原则的实际运用。

1.1设计模式分类

创建型模式
结构型模式
行为型模式

UML 类图

2.设计模式

代理模式：https://www.cnblogs.com/daniels/p/8242592.html

中介隔离作用，代理类对象可以在客户类和委托对象之间起到中介的作用。
开闭原则，增加功能。代理类本身并不真正实现服务，而是同过调用委托类的相关方法，来提供特定的服务。可以通过给代理类增加额外的功能来扩展委托类的功能。
java动态代理 https://blog.csdn.net/yaomingyang/article/details/80981004

Miller-Rabin素数探测

发表于 2021-02-15 更新于 2021-09-10

Miller-Rabin素数探测

费马小定理，如果p为质数，且$gcd(a,p)=1$，那么$a^{p - 1} \equiv 1 (mod\ p)$，如果p为质数，且a，p互质，那么a的p-1次方除以p的余数等于1。

二次探测定理，如果p是素数，且x是小于p的正整数，且$x^2 \equiv 1 (mod\ p)$，那么$x = 1$或者$x =p - 1$。

Miller-Rabin素数探测，将p-1(偶数)表示为$d \times 2^r$，其中d为奇数，如果p为素数，那么存在某个$0 \le i < r$使得$a^{d*2^{r - i}} mod\ n = n - 1$，或者$a^d = 1$。

using ll = long long;
vector<int> prime{2, 3, 5};
ll qpow(ll a, ll b, ll p) {
	ll ans = 1;
	while (b) {
		if (b & 1) ans = ans * a % p;
		a = a * a % p;
		b >>= 1;
	}
	return ans;
}
// 如果是long long会发生溢出，则需要在模运算意义下计算快速积

int TwiceDetect(ll a, ll b, ll p) {
    int r = __builtin_ctz(b);
    ll d = b >> t;
    ll x, y;
    x = y = qpow(a, d, p);
    while (r--) {
        y = x * x % p;
        if (y == 1 && x != 1 && x != p - 1) return 1; //是合数返回1
        x = y;
    }
   	return y != 1;
}


bool miller_rabin(ll p) {
    if (p == 2) return true;
    if (p < 2 || p % 2 == 0) return false;
    for (int i = 0; i < 3; ++i) {
        ll base = prime[i];
        if (p == base) return true;
        if (TwiceDetect(base, p - 1, p)) return 0;
    }
    return 1;
}

线段树I

发表于 2021-02-05 更新于 2021-09-10

线段树

线段树本质上开了O(4n)的空间来维护了数组区间的性质。根节点从下标1开始

void build(int p, int l, int r) {
    // p为当前l, r区间对应的下标， l为当前区键的左侧下标，r为右侧下标
    if (l == r) {
        //更新a[p]
        return;
    }
    int mid = l + (r - l) / 2;
    build(p << 1, l , mid);
    build(p << 1 | 1, mid + 1, r);
    a[p] = f(a[p << 1], a[p << 1 | 1])
}

惰性更新，当更新区间包含了当前的区间[l, r]，只需要更新当前的节点并进行标记。

1
2
3

void update(int p, int l, int r, int ul, int ur, int val) {
    
}

可持久化并查集

发表于 2021-02-04 更新于 2021-09-10

可持久化并查集

可持久化并查集 = 可持久化 + 并查集 = 主席树 + 并查集

leetcode 1724 检查边长度限制的路径是否存在 II

主席树方便用来维护历史的版本信息，可以支持回退，访问之前版本的数据结构。

并查集，常用的两种优化方法是路径压缩，按秩合并。在可持久化并查集中只会用到按秩合并，即深度小的点向深度大的点合并，保证单次查询的时间复杂度为$ologn$

可持久化并查集进本操作，状态定义

int tot;
int rt[N] // 保存每一个版本的头结点
int ls[N << 5], rs[N << 5] // 每个节点的左右孩子
int fa[N << 5], sz[N << 5] // 节点的父亲、树的高度

建立基础主席树

void build(int &t, int l, int r) {
	t = ++tot;
	if (l == r) {
		fa[t] = l;
		return;
	}
	int mid = l + (r - l) / 2;
	build(ls[t], l, mid);
	build(rs[t], mid + 1, r);
}

查找某一个元素在主席树中的下标

int query(int t, int l, int r, int x) {
    // t为某一历史版本的根节点下标， x为待查找的元素
	if (l == r) return t;
	int mid = l + (r - l) / 2;
	if (x <= mid) return query(ls[t], l, mid, x);
	else return query(rs[t], mid + 1, r, x);
}

查找版本号为t元素x的祖先

int find(int t, int l, int r, int x) {
	int p = query(t, l, r, x); // 查询x的下标
	if (fa[p] == x) return x;
	return find(t, l, r, fa[p]);
}

按秩合并

int unite(int pre, int l, int r, int x, int father) {
    // 修改x节点的父亲为father
    int t = ++tot;
    ls[t] = ls[pre], rs[t] = rs[pre];
    if (l == r) {
        fa[t] = father;
        sz[t] = sz[pre];
        return t;
    }
    int mid = l + (r - l) / 2;
    if (x <= mid) ls[t] = unite(ls[pre], l, mid, x, father);
    else rs[t] = unite(rs[pre], mid + 1, r, x, father);
    return t;
}

更新合并后父节点的深度

void update(int t, int l, int r, int x) {
	if (l == r) {
		sz[t]++;
		return;
	}
	int mid = l + (r - l) / 2;
	if (x <= mid) update(ls[t], l, mid, x);
	else update(rs[t], mid + 1, r, x);
}

全部代码如下, java用时329ms通过了全部测试用例，但是用c++超时了…..不开o2优化太坑人了。

#pragma GCC optimize(2)
class DistanceLimitedPathsExist {
public:
    static constexpr int N = 10005;
    int tot, n;
    int rt[N], ls[N << 5], rs[N << 5], fa[N << 5], sz[N << 5];
    vector<int> dis;

    void build(int &t, int l, int r) {
        t = ++tot;
        if (l == r) {
            fa[t] = l;
            return;
        }
        int mid = l + (r - l) / 2;
        build(ls[t], l, mid);
        build(rs[t], mid + 1, r);
    }

    int query(int t, int l, int r, int x) {
        if (l == r) return t;
        int mid = l + (r - l) / 2;
        if (x <= mid) return query(ls[t], l, mid, x);
        else return query(rs[t], mid + 1, r, x);
    }

    int find(int t, int l, int r, int x) {
        int p = query(t, l, r, x); 
        if (fa[p] == x) return p;
        return find(t, l, r, fa[p]);
    }

    int unite(int pre, int l, int r, int x, int father) {
    // 修改x节点的父亲为father
        int t = ++tot;
        ls[t] = ls[pre], rs[t] = rs[pre];
        if (l == r) {
            fa[t] = father;
            sz[t] = sz[pre];
            return t;
        }
        int mid = l + (r - l) / 2;
        if (x <= mid) ls[t] = unite(ls[pre], l, mid, x, father);
        else rs[t] = unite(rs[pre], mid + 1, r, x, father);
        return t;
    }

    void update(int t, int l, int r, int x) {
        if (l == r) {
            sz[t]++;
            return;
        }
        int mid = l + (r - l) / 2;
        if (x <= mid) update(ls[t], l, mid, x);
        else update(rs[t], mid + 1, r, x);
    }


    DistanceLimitedPathsExist(int n, vector<vector<int>>& edgeList) {
        tot = 0;
        this->n = n;
        memset(rt, 0, sizeof(rt));
        memset(ls, 0, sizeof(ls));
        memset(rs, 0, sizeof(rs));
        memset(fa, 0, sizeof(fa));
        memset(sz, 0, sizeof(sz));
        sort(edgeList.begin(), edgeList.end(), [](auto a, auto b) {
            return a[2] < b[2];
        });
        build(rt[0], 0, n - 1);
        for (int i = 0; i < edgeList.size(); ++i) {
            rt[i + 1] = rt[i];
            int x = edgeList[i][0], y = edgeList[i][1];
            int posx = find(rt[i], 0, n - 1, x), posy = find(rt[i], 0, n - 1, y);
            if (fa[posx] != fa[posy]) {
                if (sz[posx] > sz[posy]) swap(posx, posy);
                rt[i + 1] = unite(rt[i], 0, n - 1, fa[posx], fa[posy]);
                if (sz[posx] == sz[posy]) update(rt[i + 1], 0, n - 1, fa[posy]);
            }
            dis.push_back(edgeList[i][2]);
        }
    }
    
    bool query(int p, int q, int limit) {
        int num = upper_bound(dis.begin(), dis.end(), limit - 1) - dis.begin();
        int version = rt[num];
        int posx = find(version, 0, n - 1, p);
        int posy = find(version, 0, n - 1, q);
        if (fa[posx] == fa[posy]) return true;
        else return false;
    }
};

主席树

发表于 2021-02-03 更新于 2021-09-10

主席树（可持久化线段树）

问题描述：

给定N个数（int范围内），一共M次询问，每次都要询问区间[[l,r]的第k大的数。其中N, M, l, r均不超过$2\times10^5$，保证询问有答案

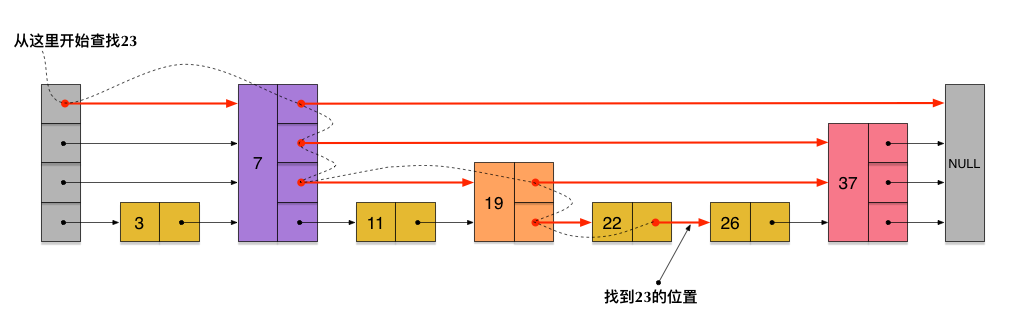
主席树本名可持久化线段树，也就是说，主席树是基于线段树发展而来的一种数据结构。其前缀”可持久化”意在给线段树增加一些历史点来维护历史数据，使得我们能在较短时间内查询历史数据，图示如下。

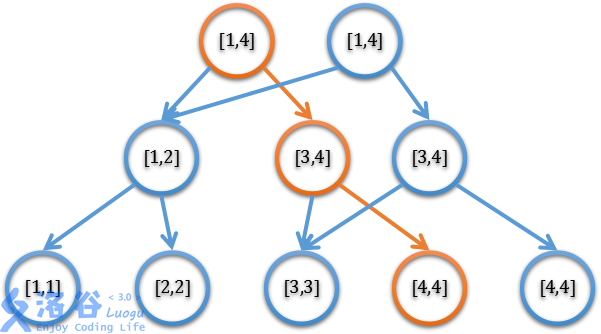
当每插入一个数据时，会修改$logn$个节点，因为主席树的左右子树节点编号不能够计算得到，而是需要记录下来。

static constexpr int N = 200010
int rt[N]                  // 记录插入第i个数后的根节点
int ls[N << 5], rs[N << 5] // 记录左儿子，右儿子
int sum[N << 5]            // 记录当前节点区间的元素个数

将数组复制一份，进行排序，去掉重复的数字离散化。
以离散化后的数组为基础建立一个全零的线段树，称为基础主席树
对原数据中每一个[1,i]区间统计，有序地插入新节点，i每增加1，就会多一个数，仅需对主席树对应的节点增加1即可
对于查询[l, r]中第k小值的操作，找到[l, r]对应的根节点，按照线段树操作的方法即可

建立基础主席树

void build(int &u, int l, int r) {
	u = ++tot;
	if (l == r) return;
	int mid = l + (r - l) / 2;
	build(ls[u], l, mid);
	build(rs[u], mid + 1, r);
}

向主席树中加入元素

int modify(int pre, int l, int r, int x) {
	int cur = ++tot;
	ls[cur] = ls[pre]; rs[cur] = rs[pre]; sum[cur] = sum[pre] + 1;
	if (l == r) return cur;
	int mid = l + (r - l) / 2;
    if (x <= mid) ls[cur] = modify(ls[cur], l, mid);
    else rs[cur] = modify(rs[cur], mid + 1, r);
	return cur;
	
}

查询区间第k大，注意区间下标是从1开始

int query(int u, int v, int l, int r, int k) {
    int ans = 0, x = sum[ls[v]] - sum[ls[u]];
    int mid = l + (r - l) / 2;
    if (l == r) return l;
    if (k <= x) ans = query(ls[u], ls[v], l, mid, k);
    else ans = query(rs[u], rs[v], mid + 1, r, k - x);
    return ans;
}