TYS的博客

算法小白努力学习中

0%

发表于 更新于 分类于

博弈

博弈的两种的分类：

  • 动态博弈是指在博弈中，两个参与人有行动的先后顺序，且后行动者能够观察到先行动者所选择的行动。

  • 静态博弈是指在博弈中，两个参与人同时选择或不同时选择时，后行动者并不知道先行动者采取什么样的具体行动。

1. 极大极小博弈树

​ 由于动态博弈参与者的行动有先后顺序，因此参与者的行动构成的为树状结构。

​ 博弈通常是双方对抗，甚至是零和的博弈。也就是说，对对方最有利的决策，反过来就是对我方最不利的局面。在轮到我们做出决策的时候，我们通常希望最大化我们的收益，叫做极大层，此时树的节点叫做极大层节点；在对手做决策的时候，对手希望最小化我们的收益，叫做极小层，此时树的节点叫做极小层节点。由于双方是交替做出决策，因此极大层、极小层通常是交替出现，这样的数据结构就叫做极大极小树（Min-Max Tree）。

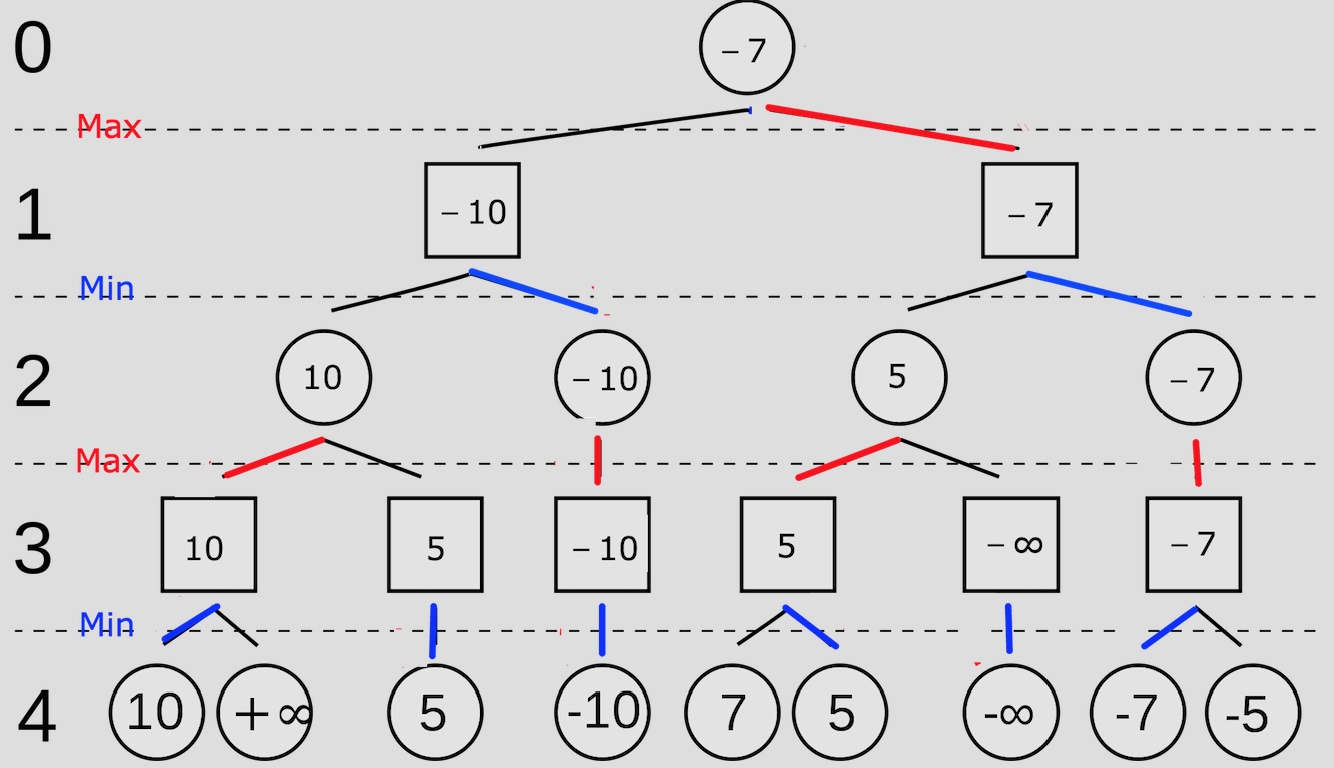
max-min-tree.png

preview

「必胜态」和「必败态」的概念：

  • 一个状态为「必胜态」，当且仅当其相邻状态中至少有一个「必败态」。这里相邻的状态的定义为：在当前状态中进行决策的玩家可以到达的所有状态。也就是说，玩家可以选择移动到一个「必败态」，使得对手必败，因此当前状态是必胜的。
  • 一个状态为「必败态」，当且仅当其相邻的所有状态都是「必胜态」。这里的道理是类似的，如果所有相邻状态都是「必胜态」，那么对手必胜，当前玩家必败。

2.从已知状态进行搜索

从已知的最终状态进行倒推之前状态的可能性，考虑已有的可能的几种状态

leetcode 913 猫和老鼠

  • 此步老鼠胜利，上一步为老鼠行动，则上一步老鼠为必胜态
  • 此步老鼠胜利，上一步为猫行动，则上一步猫行动状态的出度减一，(因为猫走该步后不肯能胜利)，只有当猫行动后所有的子状态均为老鼠的必胜态时，即出度为0时，此时猫所处的状态为必败态。
  • 此步猫胜利，上一步为猫行动，则上一步猫的状态为必胜态。
  • 此步猫胜利，上一步为老鼠行动，同上。

状态定义 f[i][j][0]为老鼠处于i，猫处于j，此时为老鼠行动，上一步为猫行动。 老鼠胜利：1， 猫胜利： 2， 平局： 0，最终返回初始状态的值。

发表于 更新于

扩展欧几里得算法

在求最大公约数时，基于一个基本的事实$(a, b) = (b, a - \lfloor \frac{a}{b}\rfloor b) = (b, a\ mod \ b)$，直到$b = 0$，此时$(a, 0) = a$。这种求最大公约数的算法叫做辗转相除法，又叫做欧几里得算法。

1
2
3
4
5
6
7
int gcd(int a, int b) {
	while (b != 0) {
		a %= b;
		swap(a, b);
	}
	return a;
}

裴蜀定理：假设$a, b$是不全为0的整数，则存在整数$x, y$使得$ax + by = gcd(a, b)$。

简单证明：
$$
gcd(a, b) = gcd(b, a\ mod\ b) = gcd(b, a - kb) = gcd(r_1, r_2) = \dots = gcd(r_n, 0)
$$
其中$r_1, r_2 \dots r_n$都可以写成$x_ia + y_ib$的形式，因此存在$ax + by = gcd(a, b)$

扩展欧几里得算法在求解最大公约数的同时，计算了一组适于裴蜀定理的系数。
递推关系的推导，$(a, b) = (b, a\ mod\ b) = (b, a - \lfloor \frac{a}{b} \rfloor b)$，因此存在四个整数$x, y, x’, y’$使得
$$
ax + by = bx’ + (a - \lfloor \frac{a}{b} \rfloor b)y’ \\
a(x - y’) + b(y - (x’ - \lfloor \frac{a}{b} \rfloor)y’) = 0 \\
x = y’, y = x’ - \lfloor \frac{a}{b} \rfloor y’
$$

1
2
3
4
5
6
7
8
9
10
11
12
ex_gcd(int a, int b, int& x, int& y) {
    if (b == 0) {
        x = 1;
        y = 0;
        return a;
    }
    int d = exgcd(b, a % b, x, y);
    int tmp = x;
    x = y;
    y = tmp - a / b * y;
    return d;
}

上述算法可以改写为迭代的形式，递推公式
$$
\left{ \begin{array}{rcl}
{\rm{x}} = y’ \\
{y = x’ - \lfloor \frac{a}{b} \rfloor y’}
\end{array} \right.
$$
将其写为矩阵的形式

$$
\left( \begin{array}{rcl}
x \\
y
\end{array} \right) = \left( \begin{array}{rcl}
0&1 \\
1&{ -\lfloor \frac{a}{b} \rfloor}
\end{array} \right)\left( \begin{array}{rcl}
{x’} \\
{y’}
\end{array} \right)
$$

  • 初始矩阵为单位矩阵
  • $
    \left( \begin{array}{rcl}
    x&m\\
    y&n
    \end{array} \right) = \left( \begin{array}{rcl}
    x&m\\
    y&n
    \end{array} \right)\left( \begin{array}{rcl}
    0&1\\
    1&{ - d}
    \end{array} \right) = \left( \begin{array}{rcl}
    m&{x - dm}\\
    n&{y - dn}
    \end{array} \right)$
  • 当b=0时，计算结束，此时x, y为满足裴蜀定理的系数，最大公约数为a。

发表于 更新于 分类于

乘法逆元

1. 逆元的定义

如果一个线性同余方程$ax \equiv 1 (mod\ b)$，则称$x$为$a\ mod\ b$的逆元，记作$a^{-1}$。

模运算规则与基本四则运算类似，但是除法例外。在ACM竞赛中，除法取模的运算要用到求逆元，从而得到$(a / b) \% c = (a * x) \% c$

证明：已知$(b * x) \% c = 1$，假设$(a / b) \% c = y_1, (a * x) \% c = y_2$

则

  • $a / b = k_1*c + y_1\quad(1)$
  • $a*x = k_2 * c + y_2\quad(2)$
  • $(1) -(2)$$\quad \rightarrow \quad a/b - a*x = (k_1 - k_2)*c + (y_1 - y_2)$
  • 左右同时乘以b $\quad \rightarrow \quad$ $a - a * x * b = k * c * b + (y1 - y2) * b$
  • 左右模上c $\quad \rightarrow \quad (y1 - y2) * b \% c = 0$
  • 因为$b \neq 0$, 所以$y_1 = y_2$

2. 求逆元

费马小定理，若p为素数，且$gcd(a, p) = 1$，则$a^{p - 1} \equiv 1 (mod\ p)$

证明：

  • 构造一个序列$A={1, 2, 3, \dots p - 1}$， 这个序列有如下的性质:
  • $\mathop{\Pi}\limits_{i = 1}^{n}A_i = \mathop{\Pi}\limits_{i = 1}^{n}(A_i \times a)$
  • 对于任意$i, j \in n $，$(A_i * a )\% p \neq (A_j * a )\% p$，因为$(A_i - A_j) * a \% p = 0$，则$A_i - A_j = 0$
  • 因此$(p - 1)! \equiv (p - 1)! * a^{p - 1}\ (mod\ p) \quad \rightarrow a^{p - 1} \equiv 1 \ mod(\ p)$

2.1 扩展欧几里得算法

扩展欧几里得算法

求解同余方程$ax \equiv 1 (mod\ b)$的最小整数解

假设采用扩展欧几里得算法求得一组$x_0, y_0$满足$ax_0 +by_0 = gcd(a, b)$，则该方程的任意解可以表示为$x = x_0 + bt, y = y_0-at$，对于任意t均成立，最小整数解可以表示为$x = ((x_0\ mod\ b) + b) mod\ b$

2.2快速幂算法

根据费马小定理，$1 \equiv a^{p -1} (mod\ p)$，因此$x = a^{p - 2}$，可以采用快速幂算法进行计算。

1
2
3
4
5
6
7
8
9
10
11
ll qpow(long long a, long long b) {
    ll ret = 1;
    while (b) {
        if (b & 1) {
            ret = (ret * a) % mod;
        }
        b >>= 1;
        a = (a * a) % mod;
    }
    return ret;
}

2.3 线性求逆元

求出$1, 2, \dots, n$中每个数关于p的逆元。

  • 显然$1{-1} \equiv 1 (mod\ p)$
  • 令$k = \lfloor\frac{p}{i} \rfloor, j = p\ mod\ i$, 因此有$p = ki + j$，在模p的意义下就有$ki + j \equiv 0\ (mod\ p)$
  • 左右同乘以$i^{-1}, j^{-1}$，有$kj^{-1} + i^{-1}=0$
  • $i^{-1}=-kj^{-1} = (p - k)j^{-1}$
1
2
3
4
5
6
7
8
static const expr mod = 1e9 + 7;
ll fac[N], R[N], inv[N];
fac[0] = fac[1] = R[0] = R[1] = inv[0] = inv[1] = 1;
for (int i = 2; i <= n; ++i) {
	fac[i] = 1LL * fac[i - 1] * i % mod;
    inv[i] = 1LL * (mod - mod / i) * inv[mod % i] % mod;
    R[i] = 1LL * R[i - 1] * inv[i] % mod;
}
1
2
3
4
ll comb(int n, int m) {
	if (n < m) return 0;
	return 1LL * fac[n] * R[m] % mod * R[n - m] % mod;
}

2.4 线性求任意n个数的逆元

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
using LL = long long;
static constexpr LL mod = 99997867;
static constexpr int N = 1000005;
LL fac[N], rf[N];

LL qpow(LL a, LL b) {
    LL ret = 1;
    while (b) {
        if (b & 1) {
            ret = ret * a % mod;
        }
        b >>= 1;
        a = a * a % mod;
    }
    return ret;
}

void init() {
    fac[0] = 1;
    for (int i = 1; i < N; ++i) {
        fac[i] = fac[i - 1] * i % mod;
    }
    rf[N - 1] = qpow(fac[N - 1], mod - 2);
    for (int i = N - 2; i >= 0; --i) {
        rf[i] = rf[i + 1] * (i + 1) % mod; 
    }
}

LL comb(int n, int m) {
    if (n < m || m < 0) return 0;
    return fac[n] * rf[n - m] % mod * rf[m] % mod;
}

发表于 更新于 分类于

洗牌算法

给你一个整数数组 nums ，设计算法来打乱一个没有重复元素的数组。

int [] shuffle()返回数据随机打乱后的结果。

打乱的概念

  • 随机打乱后的结果能够覆盖所有的情况，比如数组元素的个数为n，那么打乱后的结果应该覆盖$n!$种所有可能的结果

  • 所有结果等概率出现

方法一 暴力

暴力的方法就是模拟，假设数组中的每个元素为一个小球，我们将其放入袋子中，进行不放回的抽取，直到袋子中没有小球，我们将抽取出来的小球按顺序排列得到一个排列组合，这个排列组合出现的概率为$\frac{1}{n!}$，因此这个 数组的每个排列组合都是等概的，算法时间复杂度$O(n2)$，vector<int>的erase()删除操作是O(n)的。

对于某一个排列组合其出现概率为
$$
\mathop{\Pi}\limits_{k = 0}^{n - 1}\frac{1}{n - k} = \frac{1}{n!}
$$

方法二 Fisher-Yates算法

Fisher-Yates 洗牌算法跟暴力算法很像。在每次迭代中，生成一个当前数组末尾指针下标的随机整数。接下来，将当前元素和随机选出的下标所指的元素互相交换，这步模拟了每次从袋子里面摸一个元素的过程。

1
2
3
4
5
6
7
8
vector<int> shuffle(vector<int>& arr) {
    int n = arr.size();
    for (int i = n - 1; i >= 0; --i) {
        int pos = rand() % (i + 1);
        swap(arr[i], arr[pos]);
    }
    return arr;
}

发表于 更新于 分类于

凸优化

leetcode 1515 服务中心的最佳位置

一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标，并希望能够以此为依据为新的服务中心选址：使服务中心 到所有客户的欧几里得距离的总和最小 。给你一个数组 positions ，其中 positions[i] = [xi, yi] 表示第 i 个客户在二维地图上的位置，返回到所有客户的 欧几里得距离的最小总和

该问题本质上优化的函数如下：
$$
f(x_c, y_c) = \sum\limits_{i = 0}^{n - 1}\sqrt{(x_c - x_i)^2 + (y_c - y_i)^2}
$$
其中$(x_c, y_c)$为服务器中心的位置，其可以使$f(x_c, y_c)$取得最小值。该函数是凸函数，凸优化问题的局部最优解就是全局最优解。

1.凸集

$C$是凸集，如果对于任意的$x,y\in C$和任意的$\theta \in \mathbb{R}$且满足$0 \le \theta \le 1$时，$\theta x + (1 - \theta) y$恒成立。

2.凸函数

2.1 凸函数定义

定义在$\mathbb{R}^n \rightarrow \mathbb{R}$上的函数$f$是凸函数， 当且仅当它的定义域$\mathbb{D}(f)$是一个凸集，且对于任意的$x, y \in \mathbb{D}$和$ 0 \le \theta \le 1$， $f(\theta x + (1 - \theta)y) \le \theta f(x) + (1 - \theta)f(y)$恒成立。

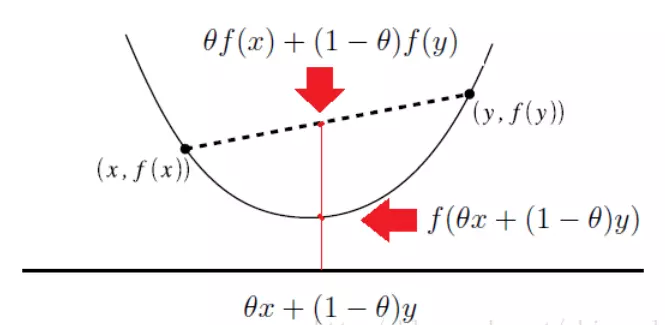
convex.jpg

2.2 凸函数的一阶充要条件

假设定义在$\mathbb{R}^n \rightarrow \mathbb{R}$上的函数$f$可微， 即对于所有的$x \in \mathbb{D}(f)$，梯度$\nabla f(x)$均存在，则函数$f$是凸函数当且仅当函数定义域$\mathbb{D}(f)$是一个凸集合，且对于所有$x, y \in \mathbb{D}(f)$均满足：
$$
f(y) \ge f(x) + \nabla f(x)^T(y - x)
$$

2.3 凸函数的二阶充要条件

记凸函数$f$的一阶导数和二阶导数分别为$g$和$H$
$$
\nabla f = \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2}\\ \vdots \\ \frac{\partial f}{\partial x_n} \end{bmatrix} \quad
H = \nabla^2f = \begin{bmatrix} \frac{\partial^2f}{\partial x_1^2} & \frac{\partial^2f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2f}{\partial x_1 \partial x_n} \\ \frac{\partial^2f}{\partial x_2 \partial x_1} & \frac{\partial^2f}{\partial x_2^2} & \cdots & \frac{\partial^2f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2f}{\partial x_n \partial x_1} & \frac{\partial^2df}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2f}{\partial x_n^2} \end{bmatrix}
$$
$f$在$x_k$处的二阶泰勒展开为
$$
f(x) = f(x_k) + \nabla f^T (x - x_k) + \frac{1}{2!}(x - x_k)H(x_k)(x - x_k) + o^n
$$
假设定义在$\mathbb{R}^n \rightarrow \mathbb{R}$上的函数$f$二阶可微， 即对于所有的$x \in \mathbb{D}(f)$，海森矩阵$\nabla^2 f(x)$均存在，则函数$f$是凸函数当且仅当函数定义域$\mathbb{D}(f)$是一个凸集合，且对于所有$x, y \in \mathbb{D}(f)$均满足$H$为半正定矩阵。

3.凸优化

可以证明本题优化的函数$f$为$\mathbb{R}^2$的上凸函数。

  • 梯度下降

  • 模拟退火

  • 爬山算法

  • 三分搜索

3.1 梯度下降

梯度下降算法，梯度下降是机器学习中常用的一种求局部最小值的算法，对于给定点$(x, y)$，它的梯度方向是函数值上升最快的方向，因此负梯度为函数值下降的最快的方向，$-\nabla f = (-\frac{\partial f}{\partial x}, -\frac{\partial f}{\partial y})$，我们从一个初始点$(x_{start}, y_{start})$开始迭代， 每次令
$$
x \prime = x - \alpha \cdot \frac{\partial f}{\partial x} \\
y \prime = y - \alpha \cdot \frac{\partial f}{\partial y}
$$

  1. 初始点$(x_{start}, y_{start})=(\frac{\sum\limits_{i =0}^{n-1}x_i}{n},\frac{\sum\limits_{i =0}^{n-1}y_i}{n})$

  2. 学习率$\alpha = 1$

  3. 学习率衰减$\eta = 0.001$

  4. 当$(x \prime, y\prime)$与$(x, y)$的距离小于$10^{-7}$时结束迭代。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    double getMinDistSum(vector<vector<int>>& positions) {
        int n = positions.size();
        double eps = 1e-7, alpha = 1, decay = 0.001;
        double x = 0, y = 0;
        for (auto p : positions) {
            x += p[0];
            y += p[1];
        }
        x = x / n;
        y = y / n;
        auto getDis = [&](double x, double y) {
            double ans = 0;
            for(auto p : positions) {
                ans += sqrt((x - p[0]) * (x - p[0]) + (y - p[1]) * (y - p[1]));
            }
            return ans;
        };
        while (true) {
            double prex = x, prey = y;
            double dx = 0, dy = 0;
            for (auto p : positions) {
                double base = max(1e-9, sqrt((x - p[0]) * (x - p[0]) + (y - p[1]) * (y - p[1])));
                dx += (x - p[0]) / base;
                dy += (y - p[1]) / base;
            }
            x -= alpha * dx;
            y -= alpha * dy;
            alpha = alpha * (1 - decay);
            if (sqrt((x - prex) * (x - prex) + (y - prey) * (y - prey)) < eps) {
                break;
            }
        }
        return getDis(x, y);
    }
};

整体写下来，尝试了很多次，初始值与学习率与学习率衰减的设置都会很大程度上影响是否能够收敛到最优值。该算法对初始化参数设置的依赖较大。

3.2 爬山算法

如果给定的凸函数很难求导，我们注意到负梯度方向，$\nabla f = -\frac{\partial f}{\partial x}(1, 0) -\frac{\partial f}{\partial y}(0, 1)$，开始我们选择一个步长，表示每次移动的距离。如果我们当前在位置$(x, y)$，我们一次枚举四个方向，判断其函数值是否更小，如果更小则进行移动，否则说明我们的步长过大，直接跳过了最优值点，调整步长为原来的一半，直到步长小于给定的阈值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    double getMinDistSum(vector<vector<int>>& positions) {
        int n = positions.size();
        double eps = 1e-8, step = 100;
        double x = 0, y = 0;
        for (auto p : positions) {
            x += p[0];
            y += p[1];
        }
        x /= n;
        y /= n;
        auto getDis = [&](double x, double y) {
            double ans = 0;
            for (auto p : positions) {
                ans += sqrt((x - p[0]) * (x - p[0]) + (y - p[1]) * (y - p[1]));
            }
            return ans;
        };
        vector<vector<int>> dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        double d = getDis(x, y);
        while (step > eps) {
            bool flag = false;
            for (int k = 0; k < 4; ++k) {
                double nx = x + step * dir[k][0], ny = y + step * dir[k][1];
                double t = getDis(nx, ny);
                if (t < d) {
                    x = nx;
                    y = ny;
                    d = t;
                    flag = true;
                    break;
                }
            }
            if (!flag) step /= 2;
        }
        return d;
    }
};

发表于 更新于 分类于

并查集

并查集可以说在算法中应用很广泛，最主要用来判断图的连通性的问题。之前做的题很少包含按秩合并，最多就是按照两个连通分量的大小进行合并。今天第一次碰到了按照秩进行合并的并查集问题，leetcode 399 除法求值，描述如下：

给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。

另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。

输入：equations = [[“a”,”b”],[“b”,”c”]], values = [2.0,3.0], queries = [[“a”,”c”],[“b”,”a”],[“a”,”e”],[“a”,”a”],[“x”,”x”]]
输出：[6.00000,0.50000,-1.00000,1.00000,-1.00000]

1.深度优先搜索

因为数据规模不大，a / b = 2，可以表示为a到b有一条权值为2的边，b到a有一条权值为0.5的边，因此对于每一个查询，可以采用深度优先搜索的方式进行查找，记录路径与当前的乘积，时间复杂度为O(n)。

2.并查集方法

  • a / b = 2.0 说明a 与 b在一个集合中，a = 2b

image-20210106122627884.png

  • 带路径压缩的查询
    $$
    w[x] = \frac{v[x]}{v[father} \
    w[x] = \frac{v[x]}{v[fa[x]]} * \frac{v[fa[x]]}{v[father]} \
    w[x] = w[x] * w[fa[x]]
    $$
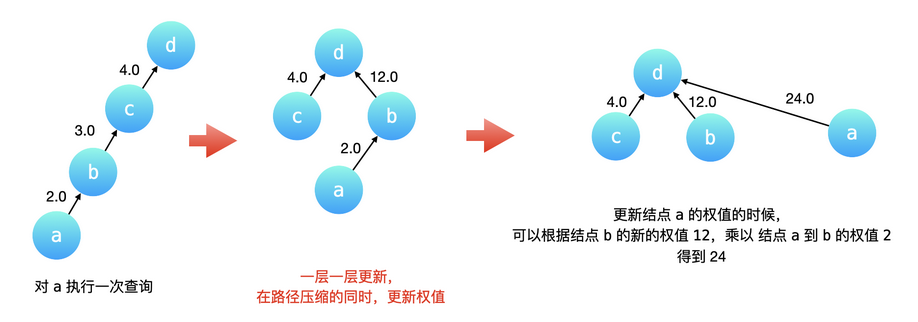
    image-20210106123132585.png

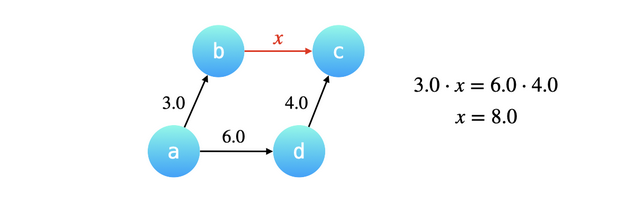
  • 按秩合并

    合并两个节点的父亲，要更新两个父亲之间的权值。
    $$
    w[fx] = \frac{v[fx]}{v[fy]} \
    w[fx] = \frac{v[x]}{w[x]} / \frac{v[y]}{w[y]} \
    $$

image-20210106123812935.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class UnionFind {
private:
    int n;
    vector<int> fa;
    vector<double> w;
public:
    UnionFind(int _n) : n(_n), fa(n, 0), w(n, 1.0) {
        for (int i = 0; i < n; ++i) fa[i] = i;
    }

    int find(int x) {
        if (x != fa[x]) {
            int father = find(fa[x]);
            w[x] *= w[fa[x]];
            fa[x] = father;
        }
        return fa[x];
    }

    void unite(int x, int y, double weight) {
        int fx = find(x), fy = find(y);
        if (fx == fy) return;
        fa[fx] = fy;
        w[fx] = weight * w[y] / w[x];
    }
    
    double isConnected(int x, int y) {
        int fx = find(x), fy = find(y);
        if (fx == fy) {
            return w[x] / w[y];
        } else {
            return -1;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        unordered_map<string, int> mp;
        int idx = 0, n = equations.size();
        UnionFind uf(2 * n);
        for (int i = 0; i < n; ++i) {
            string s = equations[i][0], t = equations[i][1];
            if (!mp.count(s)) mp[s] = idx++;
            if (!mp.count(t)) mp[t] = idx++;
            uf.unite(mp[s], mp[t], values[i]);
        }
        vector<double> ans;
        for (auto p : queries) {
            if (!mp.count(p[0]) || !mp.count(p[1])) ans.push_back(-1.0);
            else ans.push_back(uf.isConnected(mp[p[0]], mp[p[1]]));
        }
        return ans;
    }
};

发表于 更新于 分类于

洛谷p1122 最大子树和

题目中给出了N个点的权值，与N-1条边的连接关系，并未给出根。

$1 \le N \le 16000$

开始总是想需不需要换根，该题本质上是求树上点 权值和最大的一个连通分量，因此选择哪个点为根对结果没有影响，任一连通分量在某一时刻总是可以视为一颗以某个点为根的数。
$$
f[u] += max(f[v], 0) \
ans = max(ans, f[u])
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<iostream>
#include<cstdio>
#include<climits>

using namespace std;
int f[16005], s[16005], head[40000], tot, ans = INT_MIN;

struct edge{
	int to, nxt;
} e[40000];

void add(int u, int v) {
	e[++tot] = {v, head[u]};
	head[u] = tot;
}

void dfs(int u, int fa) {
	f[u] = s[u];
	for (int i = head[u]; i; i = e[i]. nxt) {
		int v = e[i].to;
		if (v == fa) continue;
		dfs(v, u);
		f[u] += max(f[v], 0);
	}
	ans = max(ans, f[u]);
}

int main(int argc, char *argv[]) {
	ios::sync_with_stdio(false);
	int n;
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> s[i];
	}
	int u, v;
	for (int i = 0; i < n - 1; ++i) {
		cin >> u >> v;
		add(u, v);
		add(v, u);
	}
	dfs(1, 0);
	cout << ans << endl;
	return 0;
}

洛谷 p1613 跑路

题目大意，图结构，如果i到j的距离为$2^k$千米，那么只需要1s时间。

$n \le 50, m \le 10000$

因为涉及到$2^k$，因此为倍增算法，先进行预处理，状态表示f[i][j][k]表示i到j有一条距离为$2^k$的边。
$$
f[i][j][k] = f[i][l][k - 1] && f[l][j][k - 1] \
1 \le l \le n
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>

using namespace std;
int dis[60][60];
bool f[60][60][65];
int n, m;

void work() {
    for (int l = 1; l <= 64; ++l) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                for (int k = 1; k <= n; ++k) {
                    f[i][j][l] = f[i][k][l - 1] && f[k][j][l - 1];
                    if (f[i][j][l]) {
                        dis[i][j] = 1;
                        break;
                    }
                }
            }
        }
    }
}

void floyd() {
    for (int k = 1; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
            }
        }
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin >> n >> m;
    memset(dis, 63, sizeof(dis));
    int u, v;
    for (int i = 0; i < m; ++i) {
        cin >> u >> v;
        dis[u][v] = 1;
        f[u][v][0] = true;
    }
    work();
    floyd();
    cout << dis[1][n] << endl;
    return 0;
}

发表于 更新于 分类于

洛谷P2014 选课

在大学里每个学生，为了达到一定的学分，必须从很多课程里选择一些课程来学习，在课程里有些课程必须在某些课程之前学习，如高等数学总是在其它课程之前学习。现在有 NNN 门功课，每门课有个学分，每门课有一门或没有直接先修课（若课程 a 是课程 b 的先修课即只有学完了课程 a，才能学习课程 b）。一个学生要从这些课程里选择 MMM 门课程学习，问他能获得的最大学分是多少？

每门课只有一门先修课， 因此该图结构为森林，假设没有选修课的父节点都指向零，因此如果要选择子节点，则必须要选择父节点，因为父节点为选修课的要求。

转换为树上背包问题
$$
dp[i][j] = max(dp[i][j], dp[i][j - k] + dp[x][k]) \quad x为i的子节点。
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;
int f[305][305], head[305], tot, scores[305], sz[305];

struct edge{
	int to, nxt;
} edges[305];

void add(int u, int v) {
	edges[++tot] = {v, head[u]};
	head[u] = tot;
}

void dfs(int u) {
	sz[u] = 1;
	f[u][1] = scores[u];
	for (int i = head[u]; i; i = edges[i].nxt) {
		int v = edges[i].to;
		dfs(v);
		sz[u] += sz[v];
		for (int j = sz[u]; j >= 1; --j) {
			for (int k = min(j - 1, sz[v]); k >= 0; --k) {
				f[u][j] = max(f[u][j], f[u][j - k] + f[v][k]);
			}
		}
	}
}

int main(int argc, char *argv[]) {
	int n, m;
	cin >> n >> m;
	int k, s;
	for (int i = 1; i <= n; ++i) {
		cin >> k >> scores[i];
		add(k, i);
	}
	dfs(0);
	cout << f[0][++m] << endl;  //注意包含了0节点，因此要多选一门
	return 0;
}

发表于 更新于 分类于

树与图上的动态规划

洛谷p 2015 二叉苹果树

二叉树共有N个结点，编号为1-N，树根编号一定是1。每颗树枝上有一定数量苹果，给定需要保留的树枝数量，求出最多能留住多少苹果。

$1\le N, Q \le 100$

通常定义图的方式为：e[tot]记录了某条边的连接信息，head[u]记录了边的序号。

1
2
3
4
5
6
7
8
struct edge {
	int to, nxt, w;
} e[MAXN];

void add(u, v, w) {
	e[++tot] = {v, head[u], w};
    head[u] = tot;
}

状态定义：

1
f[u][i]表示u的子树上保留i条边，最多可保留的苹果数目

状态转移方程，n颗树的01背包问题。
$$
f[u][i] = max(f[u][i], f[u][i - j - i] + f[v][j] + e[u->v].w)
$$
保留一条边必须保留从根节点到这条边路径上的所有边，若果要保留子树v上的边，那么必须保留u到v的这条边。

整体代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<iostream>
#include<algorithm>
#include<cstdio>

using namespace std;

int n, rem, tot;	
int f[105][105], sz[105], head[105];
struct edge {
	int to, nxt, w;
} e[105 << 1];

void add(int u, int v, int w) {
	e[++tot] = {v, head[u], w};
	head[u] = tot;
}

void dfs(int u, int fa) {
	for (int i = head[u]; i; i = e[i].nxt) {
		int v = e[i].to;
		if (v == fa) continue;
		dfs(v, u);
		sz[u] += sz[v] + 1;
		for (int j = min(rem, sz[u]); j >= 0; --j) {
			for (int k = min(j - 1, sz[v]); k >= 0; --k) {
				f[u][j] = max(f[u][j], f[u][j - k - 1] + f[v][k] + e[i].w);
			}
		}
	}
}

int main(int argc, char *argv[]) {
	ios::sync_with_stdio(false);
	cin >> n >> rem;
	int u, v, w;
	for (int i = 0; i < n - 1; ++i) {
		cin >> u >> v >> w;
		add(u, v, w);
		add(v, u, w);
	}
	dfs(1, -1);
	cout << f[1][min(sz[1], rem)] << endl;
	return 0; 
}