TYS的博客

动态规划优化-单调队列

发表于 2020-12-22 更新于 2021-09-10 分类于 Data Structure

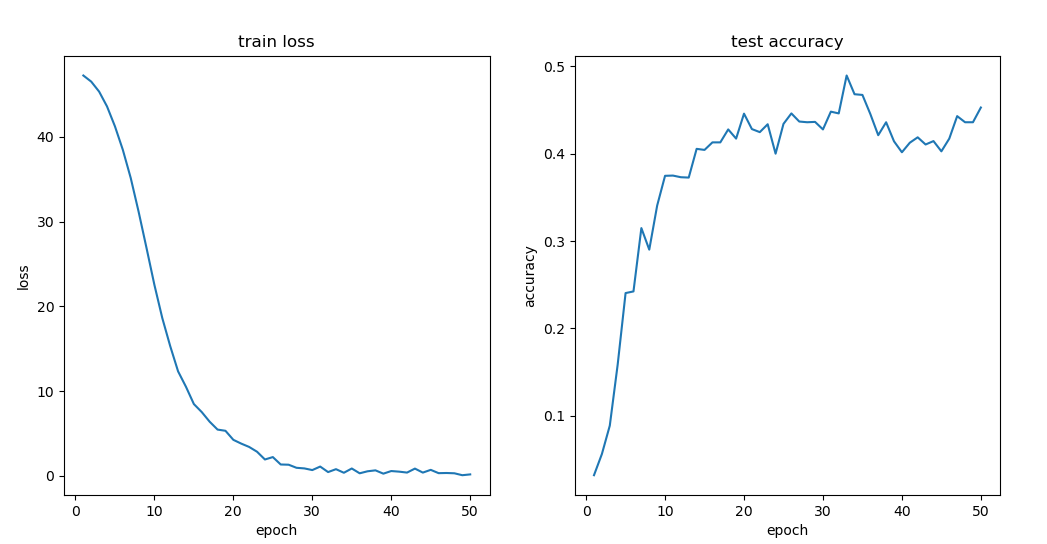
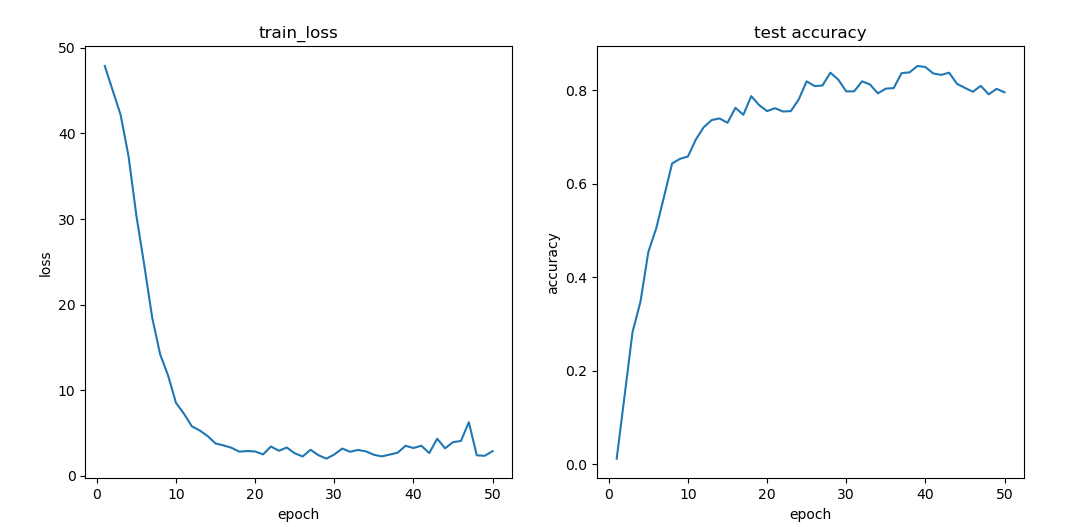
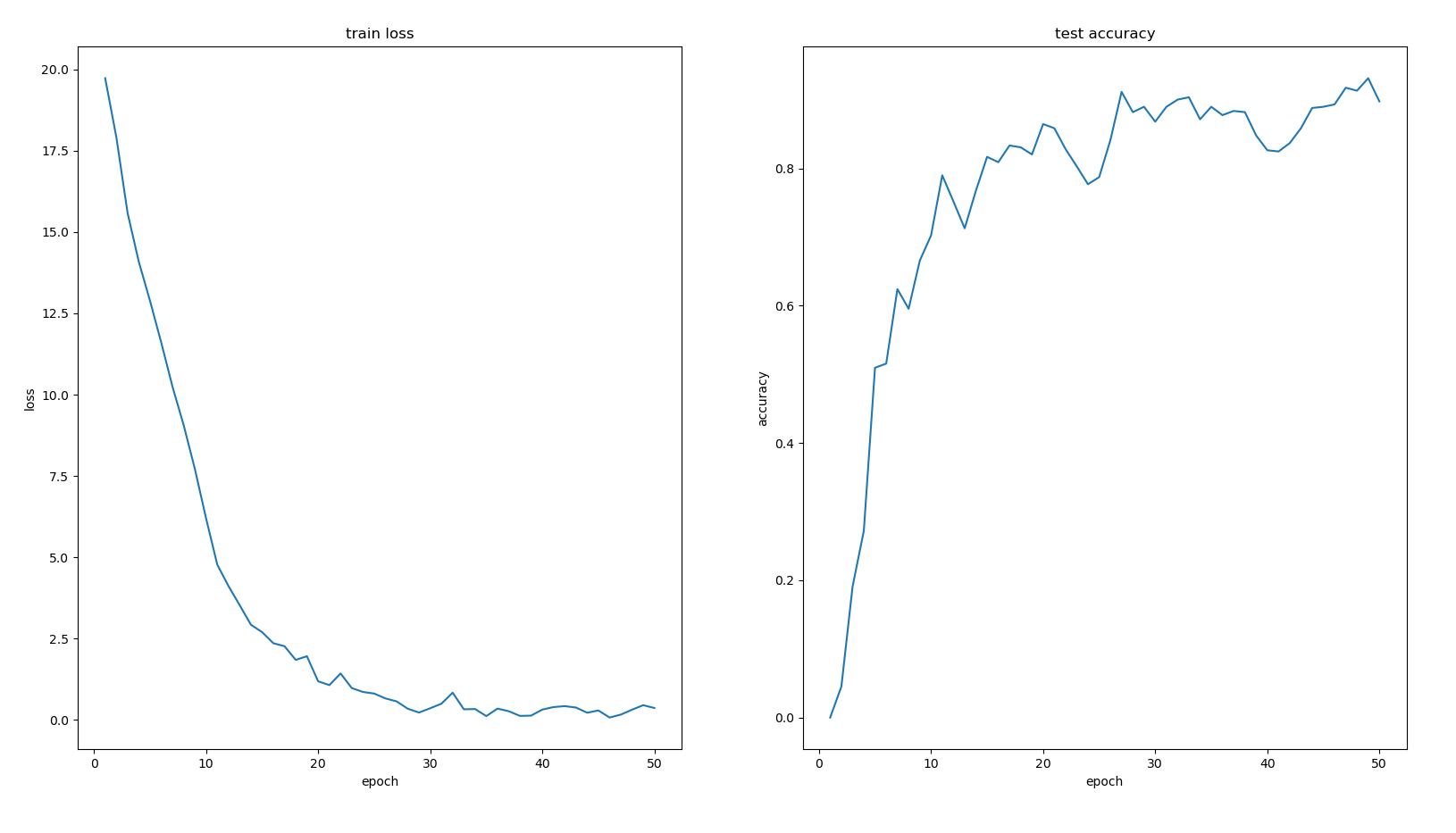
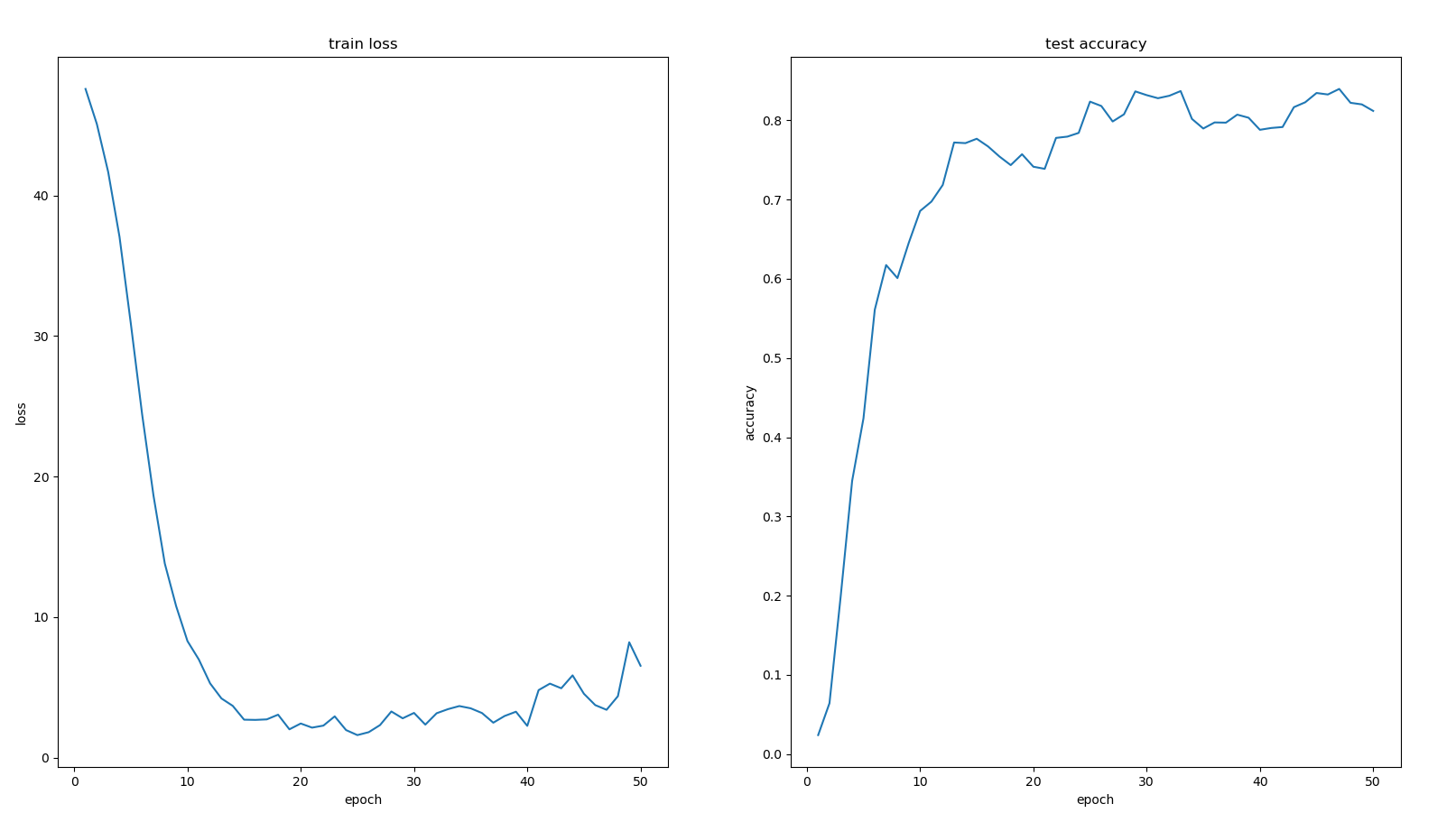
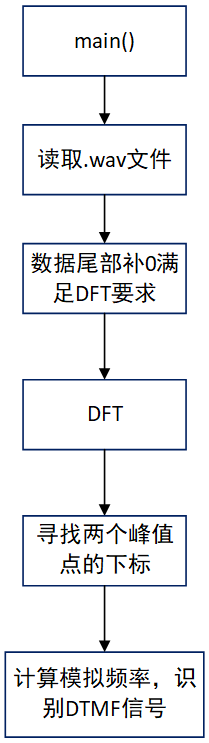
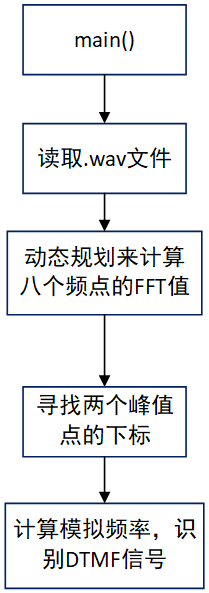
动态规划优化-单调队列

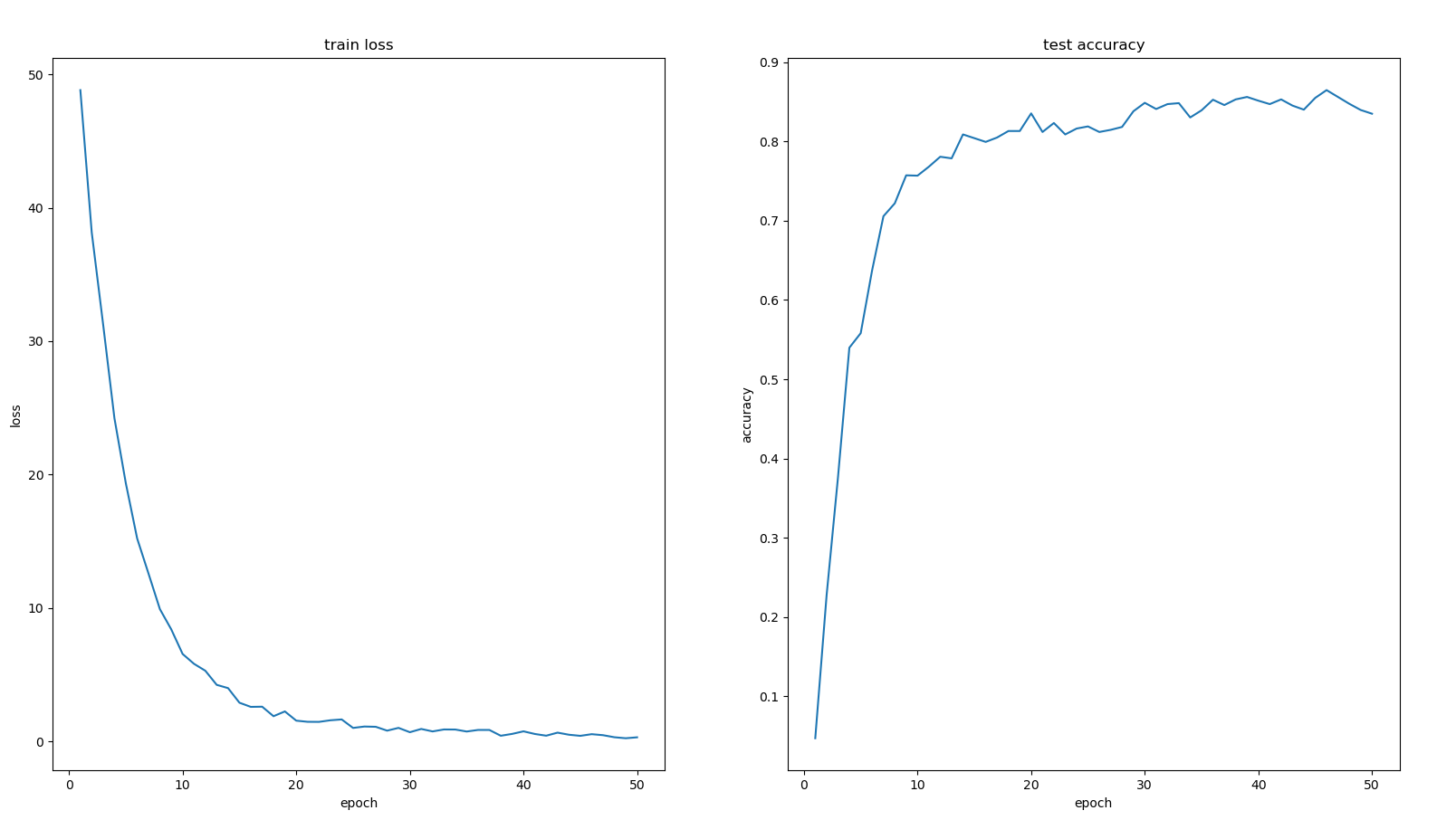
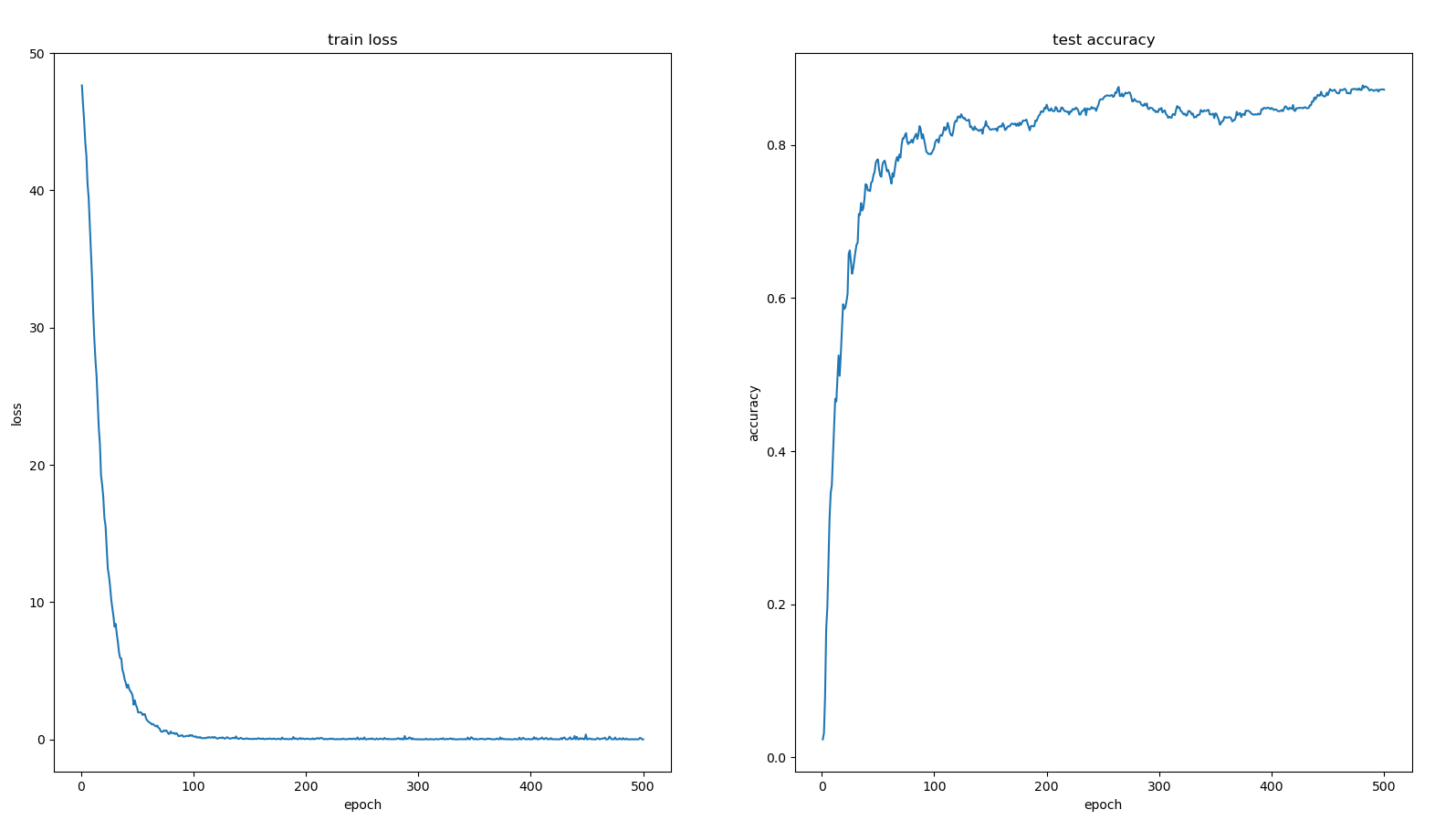
当状态转移的复杂度为$O(n)$时，状态个数为n个，动态规划的算法复杂度为$O(n^2)$，可能会超时，因此对状态转移的过程进行优化，将状态转移的复杂度降低到$O(logn)$或$O(1)$

例1 多重背包的单调队列优化

有 N 种物品和一个容量是 V的背包。第 i种物品最多有 $s_i$ 件，每件体积是 $v_i$，价值是$w_i$。求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。输出最大价值。0<N≤1000
0<V≤20000
0<$s_i$,$v_i$,$w_i$≤20000

状态转移方程，可以按照体积进行分组，本质上是求一个滑动窗口的最大值。
$$
dp[j+mv] = max(dp[j] + mw, dp[j+v] + (m - 1)w, \dots, dp[j+mv])
$$
对上面的状态转移方程进行变形,采用单调队列进行优化，代码如下：
$$
dp[j+mv] = max(dp[j], dp[j+v] - w, \dots, dp[j+mv]) + mw
$$

#include<iostream>
#include<queue>
#include<stdio.h>
#include<string.h>

using namespace std;

int dp[20010], pre[20010], dq[20010];
int  main() {
    int n, m, v, w, s;
    cin >> n >> m;

    memset(dp, 0, sizeof(dp));
    for (int i = 0; i < n; ++i) {
        cin >> v >> w >> s;
        memcpy(pre, dp, sizeof(dp));
        memset(dp, 0, sizeof(dp));
        for (int j = 0; j < v; ++j) {
            int head = 0, tail = -1;
            for (int k = j; k <= m; k += v) {
                while (head <= tail && pre[k] - pre[dq[tail]] > (k - dq[tail]) / v * w) {
                    tail--;
                }
                dq[++tail] = k;
                if ((k - dq[head]) / v > s) head++;
                dp[k] = pre[dq[head]] + (k - dq[head]) / v * w;
            }
        }
    }
    cout << dp[m] << endl;
    return 0;
}

例2 跳跃游戏VI

给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。一开始你在下标 0 处。每一步，你最多可以往前跳 k 步，但你不能跳出数组的边界, 达数组最后一个位置（下标为 n - 1 ），你的得分为经过的所有数字之和。请你返回你能得到的 最大得分 。

1 <= nums.length, k <= $10^5$
$-10^4$ <= nums[i] <= $10^4$

状态转移方程

$$
f[i]=\max_{max(0,i−k)≤j<i}{f[j]}+nums[i]
$$

该状态转移方程为$O(n^2)$，但是我们仅需要前面这个滑动窗中的最大值，因此采用单调队列的方式进行优化，使得队列头部为该滑动窗的最大值。

class Solution {
public:
    int maxResult(vector<int>& nums, int k) {
        int n = nums.size();
        deque<int> dq{0};
        vector<int> dp(n, 0);
        dp[0] = nums[0];
        for (int i = 1; i < n; ++i) {
            if (i - dq.front() > k) dq.pop_front();
            int val = dp[dq.front()] + nums[i];
            while (!dq.empty() && val > dp[dq.back()]) {
                dq.pop_back();
            }
            dq.push_back(i);
            dp[i] = val;
        }
        return dp[n - 1];
    }
};

leetcode 418 屏幕可显示句子的数量

发表于 2020-12-20 更新于 2021-09-10 分类于 Data Structure

题目描述

给你一个 rows x cols 的屏幕和一个用非空的单词列表组成的句子，请你计算出给定句子可以在屏幕上完整显示的次数。

单词不能拆分成两行。

单词在句子中的顺序必须保持不变。

在一行中的两个连续单词必须用一个空格符分隔。

句子中的单词总量不会超过 100。

每个单词的长度大于 0 且不会超过 10。

1 ≤ rows, cols ≤ 20,000.

方法1 暴力模拟(超时）

开始看这道题没什么思路，放置单词这个应该没有什么规律，只能去暴力计算放置字符串的位置，模拟了一下在pos这个位置放置一个句子，下一次放置该句子的位置与行数。无奈被这个数据给卡了[“a”], 20000, 20000，按句子模拟必然超时。

方法2 动态规划

这道题的trick在于单词数量比较少，不超过100个，并且当单词不能放入当前行时，下一次其一定放置在下一行的行首。这样可以定义两个状态，这样预处理的时间复杂度为$O(mN)$, 计算放置句子个数的过程时间复杂度为$O(N)$
$$
count[j] \quad 以第j个单词为当前行第一个单词时，放置的句子的个数 \
next[j] \quad 以第j个单词为当前行第一个单词时，下一行第一个单词
$$

class Solution {
public:
    int wordsTyping(vector<string>& sentence, int rows, int cols) {
        int n = sentence.size();
        vector<int> cnt(n, 0), next(n, 0);
        vector<int> arr;
        for (string s : sentence) {
            arr.push_back(s.size());
        }
        for (int i = 0; i < n; ++i) {
            int tmp = 0, idx = i;
            for (int j = 0; j <= cols + 1;) {
                j += arr[idx] + 1;
                if (j > cols + 1) break;
                if (idx == n - 1) tmp++;
                idx = (idx + 1) % n;
            }
            cnt[i] = tmp;
            next[i] = idx;
        }
        int ans = 0, idx = 0;
        for (int i = 0; i < rows; ++i) {
            ans += cnt[idx];
            idx = next[idx];
        }
        return ans;
    }

手写字符识别

发表于 2020-12-19 更新于 2021-09-10 分类于深度学习

计算机视觉(computer Vision)

1.全连接与CNN模型比较

好久没弄过深度学习的东西了，上次写得时候应该是大三上学期，一转眼就是两年了。感觉自己的记忆力好差啊，之前搞得那些已经是忘得一干二净了。这次的任务是采用Omniglot数据集进行手写数字的识别，该数据及包含了50中字母系统中共计1623种字符，每个字符有20个样本，部分样本如下图所示。

我采用的深度学习框架是pytorch，当用户使用DataLoader加载自定义数据时，需要继承Dataset这个类，并重写其中的两个方法。传入参数为图片路径与标签的字典。采用DataLoader()加载数据，batch_size大小设置为64。

def __getitem__(self, index):
	raise NotImplementedError
def __len__(self):
	raise NotImplementedError

定义包含一个隐层的全连接模型, 训练50个epoch，训练集上的loss与测试集上的accuracy如下图所示，全连接模型测试集的准群率在40%左右。

model = nn.Sequential(
    nn.Linear(784, 2048),
    nn.ReLU(),
    nn.Linear(2048, 50),
)

定义包含四个卷积层与两个全连接层的CNN网络，训练50次，测试集上的最高准确率为0.8389，相比于全连接模型，准确率大大提升。

def forward(self, x):
    x = self.conv1(x)
    x = self.conv2(x)
    x = self.conv3(x)
    x = self.conv4(x)
    x = x.view(x.size(0), -1)  # (batch_size, size)
    output = self.out(x)
    return output

2.尝试与对比

2.1数据集的划分

将类别设置为20类，每个类别训练集为15个样本，测试集为3个样本，结果如下图所示，分类准确率相比于50类明显提升，最高为0.9314。适当的减少分类类别可以提升模型的分类准确率。

2.2改变模型结构

相比于示例给出的卷积网络，再加入一卷积层，结果如下，分类准确率变化不大。

2.3 不同的优化器比较

上述训练都是采用的SGD优化器，改为Adagrad优化器的结果如下，loss相比于SGD优化器，没有较大的波动。准确率相比于SGD也有较大的提升，最高为0.8647。

采用Adam优化器结果如下所示，其收敛速度慢于Adagrad优化器，训练500个epoch结果如下。测试集上的分类准确率为0.8777

进程

发表于 2020-12-18 更新于 2021-09-10 分类于 Linux

进程

1.进程的概念

程序(program)是一个存储在磁盘上某个目录中的可执行文件，内核使用exec函数将程序读入内存，并执行程序。

程序执行的实例被称为进程(process), unix系统确保每个进程都有一个唯一的数字标识符，称为进程ID

2.进程环境

进程命令行参数，当执行一个程序时，在调用main函数前先调用一个特殊的启动例程，启动例程从内核获得命令行参数和环境变量值，之后调用main函数。POSIX.1要求argv[argc]是一个空指针，因此在参数处理的循环中可以改写为

1	for (i = 0; argv[i] != NULL; ++i)

环境表: 环境表是一个字符指针数组，其中每个指针为一个以’\0’为结尾的C字符串地址，全局变量environ环境指针为该指针数组的地址。

1	extern char **environ;

快速选择算法

发表于 2020-12-18 更新于 2021-09-10 分类于 Data Structure

快速选择算法

题目描述：在未排序的数组中找到第 k 个最大的元素。

1 2	输入: [3,2,1,5,6,4] 和 k = 2 输出: 5

快速选择算法本质上是对快速排序算法进行优化，快速排序算法是将数组进行划分，从数组中任选一个元素，调整数组使得左边元素都比它小，其4右侧元素都比它大。通过递归调用快速排序对左侧序列与右侧序列进行排序。而快速选择算法对左侧区间和右侧区间的数据个数与需要寻找的第K大的数字进行比较，选择答案所存在的区间，舍弃了另一个不需要的区间，使算法复杂度降低到$ O(n+ n/2 + n/4 +…)$期望为$O(n)$，但是在最坏的情况下每次选择的都是最大或者最小值，算法时间复杂度为$O(n^2)$。

针对题目数据，未加入随机数时间为56ms，加入随机数为16ms

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        int n = nums.size();
        return quick_select(nums, 0, n - 1, n - k + 1);
    }
    
    int quick_select(vector<int>& nums, int l, int r, int k) {
        int randPos = l + rand() % (r - l + 1);
        swap(nums[l], nums[randPos]);
        int pivot = nums[l];
        int i = l, j = r;
        while (i < j) {
            while (i < j && nums[j] >= pivot) --j;
            if (i < j) nums[i] = nums[j];
            while (i < j && nums[i] < pivot) ++i;
            if (i < j) nums[j] = nums[i];
        }
        nums[i] = pivot;
        int idx = i - l + 1;
        if (idx == k) return pivot;
        else {
            return idx < k ? quick_select(nums, i + 1, r, k - idx) : quick_select(nums, l, i - 1, k);
        }
    }
};

最小的k个数

发表于 2020-12-17 更新于 2021-09-10 分类于 Data Structure

leetcode 373 查找和最小的K对数字

题目描述：给定两个以升序排列的整形数组 nums1 和 nums2, 以及一个整数 k。定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2。找到和最小的 k 对数字 (u1,v1), (u2,v2) … (uk,vk)。

做题思路

由于题目中没有给定数据范围，开始以为是双指针问题，采用贪心策略，但是举了两个例子，指针的移动无法采用贪心的方法，如[1, 3, 100]与[2, 10, 11]，第二组为(2, 3)，第三组为(1, 10)，第一个数组的指针出现了回退，因此贪心不可行。

1.暴力做法

枚举数组1与数组2所有可能的组合，并采用箭指offer 40 最小的k个数的最大堆的方法，维护最小的k对数字，时间复杂度$O(n^2logk)$，运行时间1232ms，勉强过了。

2.利用数组的排序信息

在暴力做法中完全没有利用到题目中给出的数组为升序排列这个信息，还是以[1, 3, 100]与[2, 10, 11]为例，开始我们将$(nums1[0], nums2[j]) j = 1,2\dots n$放入最小堆中，如果当前堆中弹出的为$(nums1[i], nums2[j])$，那么则将$(nums1[i + 1], nums2[j])$放入到最小堆中。

数据结构pair<pair<int, int>, int>，分别记录nums1的值、下标， nums2的值。

最小堆 priority_queue<pair<pair<int, int>, int>, vector<pair<pair<int, int>, int>>, cmp>

struct cmp {
    bool operator ()(const pair<pair<int, int>, int>&a, const pair<pair<int, int>, int>& b) const {
        return a.first.first + a.second > b.first.first + b.second;
    }
};

class Solution {
public:
    vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
        int m = nums1.size(), n = nums2.size();
        if (m == 0 || n == 0) return {};
        priority_queue<pair<pair<int, int>, int>, vector<pair<pair<int, int>, int>>, cmp> pq;
        for (int i = 0; i < n; ++i) {
            pq.push({{nums1[0], 0}, nums2[i]});
        }
        int cnt = 0;
        vector<vector<int>> ans;
        while (!pq.empty() && cnt < k) {
            auto [a, b] = pq.top();
            pq.pop();
            ans.push_back({a.first, b});
            int idx = a.second;
            if (idx + 1 < m) pq.push({{nums1[idx + 1], idx + 1}, b});
            ++cnt;
        }
        return ans;
    }
};

最长递增子序列

发表于 2020-12-16 更新于 2021-09-10 分类于 Data Structure

最长递增子序列

leetcode 300 最长递增子序列

leetcode 673 最长递增子序列的个数

对于673题，常规做法动态规划，记录两个状态最长上升子序列的长度与当前长度对应的子序列的个数。动态规划的规划过程
$$
arr[j] > arr[i] \
if; dp[j] < dp[i] + 1 \quad dp[j] = dp[i] + 1, nums[j] = nums[i] \
else ;if ; dp[j] == dp[i] + 1 \quad nums[j] += nums[i]
$$
动态规划规划的复杂度为$O(n^2)$

采用树状数组$O(nlogn)$的复杂度，定义Node结构体，记录长度与个数，重载加法操作符。

维护小于等于当前值区间的最长长度的上升子序列个数。

struct Node {
    int m, c;
    Node (int _m, int _c) : m(_m), c(_c) {}
    Node& operator +=(Node &rhs) {
        if (m < rhs.m) {
            m = rhs.m;
            c = rhs.c;
        } else if (m == rhs.m) {
            c += rhs.c;
        }
        return *this;
    }
};

class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) {
        vector<int> arr = nums;
        sort(arr.begin(), arr.end());
        arr.erase(unique(arr.begin(), arr.end()), arr.end());
        unordered_map<int, int> mp;
        for (int i = 0; i < arr.size(); ++i) {
            mp[arr[i]] = i + 1;
        }
        vector<Node> tree(2010, {0, 0});
        Node res(0, 0);
        for (int val : nums) {
            Node tmp(0, 1);
            for (int k = mp[val] - 1; k > 0; k -= (k & -k)) {
                tmp += tree[k];
            }
            tmp.m++;
            res += tmp;
            for (int k = mp[val]; k < 2010; k += (k & -k)) {
                tree[k] += tmp;
            }
        }
        return res.c;
    }
};

DTMF信号检测与识别

发表于 2020-12-15 更新于 2021-09-10 分类于信号处理

DTMF信号的检测与识别

1. 程序设计思路与框图

1.1 FFT直接计算

利用FFT计算输入的信号的DFT频域信息，并找到两个峰值频率点，从而检测DTMF信号。

数据预处理，作业给定的为.wav文件，其中数据为16bit的short类型，文件指针偏移40个字节的位置记录了wav数据块的字节数，调用read函数将之后的数据读入到数组中。
编写类FFTMethod，调用第一次作业编写的时域基2DFT对音频信号做FFT变换。找到频域中两个峰值对应的数字角频率，从而计算得到模拟角频率，找到对应的DTMF信号
程序框图

1.2 Goertzel 算法

计算FFT包含了信号整个频域的信息，而我们只关注DTMF信号的八个特定频率，因此算法存在冗余。在FFT中如果我们只关注某一个特定的数字角频率，$X[k] = \sum_{n = 0}^{N- 1}x[m]W_n^{m -N}$，其可以视为$x[n]$通过冲激响应为$W_N^{-nk}$的LTI系统在N时刻的取值。第k个频点对应的差分方程为：
$$
V_k[n] = 2cos(\omega_k)V_k[n - 1] - V_k[n-2] + x[n] \
X_k[n] = V_k[n] - W_N^k[n - 1], v[-1] = v[-2] = 0
$$
其本质是一个动态规划的过程，由递推关系可以得到n时刻的状态，从而确定该频点的FFT。得到八个特定频点的FFT值后，选择两个峰值，从而确定DTMF信号。

1.3一串DTMF信号的识别

下图为一串DTMF信号的时域图像，可以看到其中包含了15个DTMF信号，我们要做的工作是确定每一个信号的起始于结束位置，直接使用强度值进行判断存在较大的误差，因此选择滑动窗取平均的方式。程序中选择滑动窗大小为64，计算信号每个点对应的滑动窗内的平均能量，并与阈值作比较，从而确定每一个信号的起始结束位置。之后将每一段信号采用上述的两种方法进行信号判断

程序框图

2.两种算法的结果与复杂度比较

实验结果：

复杂度分析：

FFT方法采用DFT计算了所有的频点信息，时间复杂度为$O(nlogn)$，寻找峰值的复杂度为O(n)，总的时间复杂度为$O(nlogn) + O(n)$
Goertzel方法只计算特定的8个频点，并采用差分方程的形式递推计算，时间复杂度为O(n)
FFT方法需要存储所有的频域信息，空间复杂度为$O(n)$， Goertzel方法在递推过程中只需要V[i-1]、V[i-2]这两个状态，空间复杂度为$O(1)$

unix shell简单实现

发表于 2020-12-14 更新于 2021-09-10 分类于 Linux

1.shell整体框架

github项目地址

shell程序整体框架，读取用户输入命令并执行

进入main函数后，循环执行从标准输入读取命令，解析命令，将命令字符串以空格分隔，解析为命令与参数。判断是否为内建命令(history, jobs, fb, exit)。如果不是则父进程通过fork()创建子进程，子进程执行execv()完成进程代码段与数据段内容替换。

2.输入输出重定向

定义命令结构体，其包含argc(命令参数个数)、bg(后台命令标志)、name(命令名称)、argv(命令参数)、fds(重定向文件描述符)等五个成员变量。

struct command {
    int argc;
    int bg;
    string name;
    string argv[ARG_MAX];
    int fds[2];
};

解析指令时command > file检查是否有>或<操作符，有则检查后面是否有文件，若果有文件则以读写的方式打开文件，并将返回文件描述符记录到命令结构体中，在fork()后的子进程中，采用dup2()函数将子进程的输入、输出重定向fds所指向的文件描述符。

3.实现管道

struct commands {
    string key;
    int cmd_counts;
    struct command* cmds[CMD_MAX];
    commands *pre, *next;
}

定义命令集(commands)结构体，成员cmd_counts为命令个数，cmds记录每一个解析后的命令指针。

检查输入的字符中是否有”|”，如果有按照|将字符串分隔开，并解析每一个命令(支持多条命令)
创建管道，前一个命令的stdout重定向到管道的写端，后一个命令的stdin重定向的管道的读端。
Fork()创建每一个子进程，执行指令

4.作业控制

struct job_t {
    pid_t pid;
    int jid;
    int state;
    string cmd;
};

定义job_t结构体，包含成员进程编号，作业编号，作业状态，命令字符串。定义作业运行状态：UNDEF:0、FG:1、BG:2、 ST:3

定义JOBCtrl类，来控制作业的执行。

父进程fork()创建子进程后，父进程将作业添加到作业列表，并定义SIG_CHLD信号处理函数，当子进程结束执行时，发送SIG_CH

LD信号给父进程。父进程捕捉信号，在信号处理函数中调用waitpid()函数获得子进程pid，将其从作业列表中删除。

5.后台执行程序

如果是前台执行程序，则父进程处于while循环的等待状态，直到子进程执行完毕向父进程发送SIG_CHLG信号，父进程捕捉到信号后将其从作业列表中删除后，结束while循环等待。如果是后台执行程序则打印作业相关信息并继续执行读取用户输入。

6.作业控制 jobs fg bg

jobs查看所有作业的运行状态，将作业列表中的所有作业打印输出
fg % 1，从作业列表中找到后台运行的作业，将其状态变为FG，并执行等待，直到子进程结束发出SIG_CHLD信号，从作业列表中删除。
bg % 1，父进程注册SIGTSTP信号处理，CRTL+Z, 发送STGTSTP信号给子进程，暂停子进程执行。当执行bg命令时，父进程向暂停的子进程发送SIGCONT信号恢复子进程的执行。

7.历史命令

实现了CMDCache类

哈希表+双向链表维护历史命令，哈希表记录输入字符串与解析后的命令结构体的映射，双向链表记录历史输入命令
LRU(least Recently used)算法，当输入字符串已经被解析过时，将命令从双向链表中删除，并重新命令列表头部插入。输入字符串未解析过，解析后插入列表头部。
history命令将历史命令按输入顺序的倒序排列输出
up、down命令获取上一条输入命令、下一条命令输入

动态规划优化-单调队列

例1 多重背包的单调队列优化

例2 跳跃游戏VI

题目描述

方法1 暴力模拟(超时）

方法2 动态规划

计算机视觉(computer Vision)

1.全连接与CNN模型比较

2.尝试与对比

2.1数据集的划分

2.2改变模型结构

2.3 不同的优化器比较

进程

1.进程的概念

2.进程环境

快速选择算法

做题思路

1.暴力做法

2.利用数组的排序信息

最长递增子序列

DTMF信号的检测与识别

1. 程序设计思路与框图

1.1 FFT直接计算

1.2 Goertzel 算法

1.3一串DTMF信号的识别

2.两种算法的结果与复杂度比较

1.shell整体框架

2.输入输出重定向

3.实现管道

4.作业控制

5.后台执行程序

6.作业控制 jobs fg bg

7.历史命令