TYS的博客

算法小白努力学习中

0%

发表于 更新于 分类于

1.管道的概念

管道是一种最基本的IPC机制，作用于有血缘关系的进程之间，完成数据传递，通过pipe()系统调用即可创建一个管道。

  • 其本质是一个伪文件，实为内核缓冲区
  • 两个文件描述符引用，一个表示读端，一个表示写端
  • 管道采用半双工通信方式，数据只能在一个方向流动
  • 只能在有公共祖先的进程间使用管道

2.pipe函数

1
2
3
int pipe(int (*pipefd)[2]);   
ret 0 : SUCCESS
	-1 : Failure

函数调用成功返回read/write两个文件描述符，无需open，需要手动close。

img

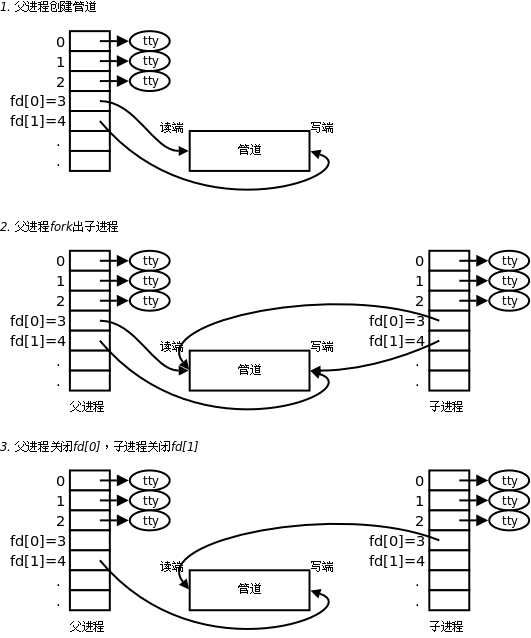
  • 父进程调用pipe函数创建管道，得到两个文件描述符fd[0]、fd[1]指向管道的读端和写端

  • 父进程调用fork()创建子进程，子进程继承父进程文件描述符。

  • 父进程关闭管道读端，子进程关闭管道写端，父进程可以向管道中写入数据，子进程将管道中数据读出。

3.管道读写行为

使用管道需要注意以下4种特殊情况

  • 如果所有指向管道写端的文件描述符都关闭了（管道写端引用计数为0），而仍然有进程从管道的读端读数据，那么管道中剩余的数据都被读取后，再次read会返回0，就像读到文件末尾一样。
  • 如果有指向管道写端的文件描述符没关闭（管道写端引用计数大于0），而持有管道写端的进程也没有向管道中写数据，这时有进程从管道读端读数据，那么管道中剩余的数据都被读取后，再次read会阻塞，直到管道中有数据可读了才读取数据并返回。
  • 如果所有指向管道读端的文件描述符都关闭了（管道读端引用计数为0），这时有进程向管道的写端write，那么该进程会收到信号SIGPIPE，通常会导致进程异常终止。当然也可以对SIGPIPE信号实施捕捉，不终止进程。具体方法信号章节详细介绍。
  • 如果有指向管道读端的文件描述符没关闭（管道读端引用计数大于0），而持有管道读端的进程也没有从管道中读数据，这时有进程向管道写端写数据，那么在管道被写满时再次write会阻塞，直到管道中有空位置了才写入数据并返回。

4.示例程序 采用管道实现 ls /home | wc

主线程调用fork()创建两个进程一个执行ls /home，另一个执行 wc，利用管道重定向两个进程的stdout，stdin。

踩坑记录，在主线程wait(NULL)前，需要手动关闭主线程的所有管道，否则第二个进程会处于读阻塞的状态，因此发生了死锁

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <errno.h>
#include <unistd.h>
#include <fcntl.h>
#include <sys/types.h>
#include <sys/wait.h>
#include <ctype.h>
#include <iostream>
using namespace std;

int main() {
    int f[2];
    pipe(f);
    for (int i = 0; i < 2; ++i) {
        pid_t pid = fork();
        if (pid == 0) {
            if (i == 1) {
                close(f[1]);
                dup2(f[0], 0);
                char *name = "/usr/bin/wc";
                char **argv = new char*[1];
                argv[0] = "/usr/bin/wc";
                int exet_st = execv(name, argv);
                close(f[0]);
                _exit(EXIT_SUCCESS);
            } else {
                close(f[0]);
                char buff[] = "test";
                write(f[1], buff, strlen(buff));
                close(f[1]);
                _exit(EXIT_SUCCESS);
            }
        }
    }
    close(f[0]);
    close(f[1]);
    for (int i = 0; i < 2; ++i) {
        wait(NULL);
    }
    return 0;
}

发表于 更新于 分类于

leetcode 1477 找两个和为目标值且不重叠的子数组

leetcode 1658 将x减小到0的最小次数

leetcode 1423 可获得的最大点数

题目中给出的数据范围$1\le arr[i]\le10^4$，因此找到一段区间和为某一个数值，可以采用双指针的方式，如果当前区域的和大于target，则移动前面的指针，直到区间和小于等于target。如果存在负数或零，则采用前缀和与哈希表的方式。

对于题目1477 其要找到满足等于给定和的最小的两个不想交的区间，采用dp[j]表示区间右端点小于等于j的最小区间长度。
$$
dp[j] = \min(dp[j - 1], j - i + 1) \
ans = \min(ans, dp[i - 1] + j - i + 1)
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int minSumOfLengths(vector<int>& arr, int target) {
        int n = arr.size();
        int i = 0, sum = 0, ans = 0x3f3f3f3f;
        vector<int> dp(n, 0x3f3f3f3f);
        for (int j = 0; j < n; ++j) {
            sum += arr[j];
            while (sum > target && i < j) {
                sum -= arr[i];
                ++i;
            }
            if (j > 0) dp[j] = dp[j - 1];
            if (sum == target) {
                dp[j] = min(dp[j], j - i + 1);
                if (i > 0) {
                    ans = min(ans, dp[i - 1] + j - i + 1);
                }
            }
        }
        return ans == 0x3f3f3f3f ? -1 : ans;
    }
};

对于1658题，首先找到一段区间和为x，然后调整两个指针的位置使得两端区间和为x

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int minOperations(vector<int>& nums, int x) {
        int n = nums.size(), ans = 0x3f3f3f3f;
        int j = n - 1, sum = 0;
        while (j >= 0 && sum < x) {
            sum += nums[j];
            --j;
        }
        ++j;
        if (sum == x) ans = n - j;
        for (int i = 0; i < n; ++i) {
            sum += nums[i];
            while (j < n && sum > x) {
                sum -= nums[j];
                ++j;
            }
            if (sum == x && j > i) {
                ans = min(ans, i + 1 + n - j);
            }
        }
        return ans == 0x3f3f3f3f ? -1 : ans;
    }
};

发表于 更新于 分类于

每个叶子节点为最小的分割区间，即为数组存储的值。

假设树的高度为k，0,1,2$\dots$k，另n为区间个数，则有$2^{k - 1} < n \le 2^k$，整棵树的节点个数有$2^{k + 1} - 1$个，通常线段树空间大小为4 * n

leetcode 1109 航班预订统计

leetcode 307 区间和检索-数组可修改

leetcode 308 二维区域和检索—可变

线段树建树

数组下标同树状数组相同，都是从1开始

1
2
3
4
5
6
7
8
9
10
void build(int l, int r, int p) {
    if(l == r) {
        d[p] = a[l];
        return;
    }
    int mid = l + (r - l) / 2;
    build(l, m, p << 1);
    build(m + 1, r, p << 1 | 1);
    d[p] = d[p << 1] + d[p << 1 | 1];
}

线段树区间查询

l，r为查询区间，cl，cr为当前区间的左右边界。

1
2
3
4
5
6
7
8
9
int query(int l, int r, int p, int cl, int cr) {
    if(cl > r || cr < l) return 0;
    else if(l <= cl && r >= cr) return d[p];
    else {
        int mid = l + (r - l) / 2, sum = 0;
        if(l <= mid) sum += query(l, r, p << 1, cl, mid);
        if(r > mid) sum += quert(l, r, p << 1 | 1s, mid + 1, cr);
    }
}

线段树的点更新$O(nlogn)$

1
2
3
4
5
6
7
8
9
10
11
12
void update(int k, int v, int l, int r, int p) {  //update(k, v, 1, n, 1)
    if(l == r) a[k] += v, d[k] += v;
    else {
        int mid = l + (r - l) / 2;
        if(k <= mid) {
            update(k, v, l, mid, p << 1);
        } else {
            update(k, v, mid + 1, r, p << 1 | 1);
        }
        d[p] = d[p << 1] + d[p << 1 | 1];
    }
}

线段树区间修改与懒惰标记

对于一个区间$[l, r]$，如果每次更新区间中的每个值，那么时间复杂度为$O(nlogn)$，为了提高更新效率，采用了mark进行标记。在递归更新过程中，当当前节点区间为待更新区间的真子集时，不再向下更新。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void push_down(int p, int len) {
    mark[p << 1] += mark[p];
    mark[p << 1 | 1] += mark[p];
    d[p << 1] += mark[p] * (len - len / 2);
    d[p << 1 | 1] += mark[p] * len / 2;
    mark[p] = 0;
}

void update(int l, int r, int val, int cl, int cr, int p) {
    if(l > cr || r < cl) return;
    else if(l <= cl && r >= cr) {
        d[p] += (cr - cl + 1) * val;
        if(cl > cr) mark[p] += d;
    } else {
    	int mid = cl + (cr - cl) / 2;
        push_down(p, cr - cl + 1);
        update(l, r, val, cl, mid, p << 1);
        update(l, r, val, mid + 1, cr, p << 1 | 1);
        d[p] = d[p << 1] + d[p << 1 | 1];
    }
}

线段树区间查询 包含懒惰标记

1
2
3
4
5
6
7
8
9
int query(int l, int r, int cl, int cr, int p) {
    if(l > cr || r < cl) return 0;
    else if(l <= cl && r >= cr) return d[p];
    else {
        int mid = l + (r - l) / 2;
	    if(mark[p]) push_down(p, cr - cl + 1);
        return query(l, r, cl, mid, p << 1) + query(l, r, mid + 1, cr, p << 1 | 1);
    }
}